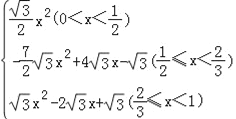题目内容
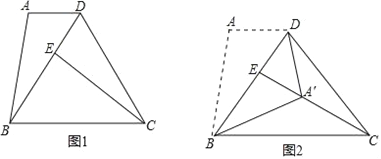
【题目】如图1,等边三角形ABC中,点D在AB上(点D与点A,B不重合),DE⊥BC,垂足为E,点P在BC上,且DP∥AC,△B′DE′与△BDE关于DP对称.设BE=x,△B′DE′与△ABC重叠部分的面积为S,S关于x的函数图象如图2所示(其中0<x<![]() ,
, ![]() ≤x<m与m≤x<n时,函数的解析式不同).
≤x<m与m≤x<n时,函数的解析式不同).
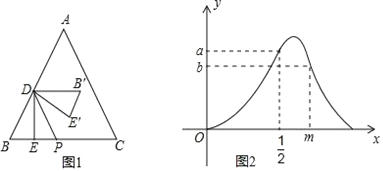
(1)填空:等边三角形ABC的边长为_____,图2中a的值为_____;
(2)求S关于x的函数关系式,并直接写出x的取值范围.
【答案】 2, ![]() ; S=
; S=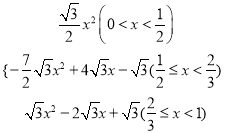
【解析】(1)先根据图象得到当x=BE=![]() 时,点B'在AC上,进而得出△ADB'是等边三角形,根据AD=DB'=DB=1,可得等边三角形ABC的边长为2,再根据S△DB'E'=S△DBE=
时,点B'在AC上,进而得出△ADB'是等边三角形,根据AD=DB'=DB=1,可得等边三角形ABC的边长为2,再根据S△DB'E'=S△DBE=![]() ,可得a的值;
,可得a的值;
(2)分三种情况讨论:当0<x<![]() 时,当
时,当![]() ≤x<
≤x<![]() 时,当
时,当![]() ≤x<1时,分别根据△B′DE′与△ABC重叠部分的形状,运用图形面积的和差关系得到S的表达式.
≤x<1时,分别根据△B′DE′与△ABC重叠部分的形状,运用图形面积的和差关系得到S的表达式.
解:(1)如图甲,
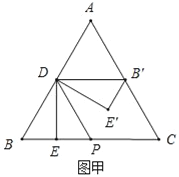
当x=BE=![]() 时,点B'在AC上,
时,点B'在AC上,
∵DE⊥BC,
∴∠BDE=30°,
∴BD=2BE=1,DE=![]() ,
,
又∵△B′DE′与△BDE关于DP对称,DP∥AC,
∴DB'=DB=1,且∠BDB'=60°×2=120°,
∴DB'∥BC,
∴△ADB'是等边三角形,
∴AD=DB'=DB=1,
∴AB=2,即等边三角形ABC的边长为2,
∵S△DB'E'=S△DBE=![]() ×
×![]() ×
×![]() =
=![]() ,
,
∴a=![]() ,
,
故答案为:2,![]() ;
;
(2)当0<x<![]() 时,如图1,
时,如图1,
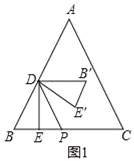
∵△ABC是等边三角形,DE⊥BC,
∴∠A=∠B=60°,∠BDE=30°,
∵△B′DE′与△BDE关于DP对称,
∴S=S△DB'E'=S△DBE=![]() BE×DE=
BE×DE=![]() x
x![]() x=
x=![]() x2;
x2;
当x=m时,点E'在AC上,此时,BE=AD=![]() AB=
AB=![]() ,即m=
,即m=![]() ,
,
当![]() ≤x<
≤x<![]() 时,如图2,
时,如图2,
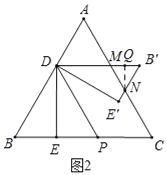
设B'D,B'E'分别与AC交于点M,N,
∵DP∥AC,
∴∠B'MN=∠DMA=∠MDP,∠BDP=∠A,
∵△B′DE′与△BDE关于DP对称,
∴∠MDP=∠BDP=∠A=60°,∠B'=∠B=60°,
∴∠B'MN=∠DMA=60°,
∴∠B'NM=60°=∠B'MN=∠B',∠ADM=60°=∠DMA=∠A,
∴△B'MN和△ADM都是等边三角形,
作NQ⊥B'M于Q,则NQ=![]() B'N,
B'N,
∵B'M=B'D﹣DM=BD﹣AD=2x﹣(2﹣2x)=4x﹣2,
∴S=S四边形DE'NM
=S△B'DE'﹣S△B'MN
=S△BDE﹣S△B'MN
=![]() x2﹣
x2﹣![]() (4x﹣2)
(4x﹣2)![]() (4x﹣2)
(4x﹣2)
=﹣![]() x2+4
x2+4![]() x﹣
x﹣![]() ;
;
当点D与点A重合时,x=BE=![]() BC=1,即n=1,
BC=1,即n=1,
当![]() ≤x<1时,如图3,
≤x<1时,如图3,
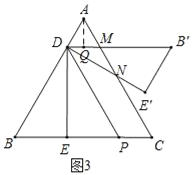
设B'D,DE'与AC分别交于点M,N,作AQ⊥DM于Q,
∵∠B'DE'=∠BDE=30°,∠ADM=60°,
∴∠ADN=90°,
∴S=S△MND
=S△ADN﹣S△ADM
=![]() (2﹣2x)
(2﹣2x)![]() (2﹣2x)﹣
(2﹣2x)﹣![]() (2﹣2x)
(2﹣2x)![]() (2﹣2x)
(2﹣2x)
=![]() x2﹣2
x2﹣2![]() x+
x+![]() .
.
综上所述,S关于x的函数关系式为:S=