题目内容
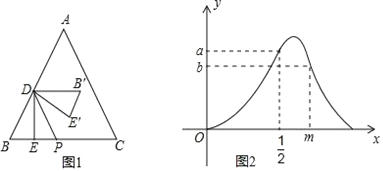
【题目】已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中,点A(11,0),点B(0,6),点P为BC边上的动点(点P不与点B,C重合),经过点O、P折叠该纸片,得点B′和折痕OP(如图①)经过点P再次折叠纸片,使点C落在直线PB′上,得点C′和折痕PQ(如图②),当点C′恰好落在OA上时,点P的坐标是_____.

【答案】![]() 或
或![]()
【解析】∵把△OPB沿OP折叠,使点C落在点C′处,
∴BP=PB′,OB=OB′=6,∠A=∠OB′P=90°,
∵把△CPQ沿PQ折叠,使点D落在直线OA上的点C′处,
∴CP=C′P,CQ=C′Q,∠PC′Q=∠C=90°,
设BP=B′P=x,则PC=PC′=11﹣x,
∵BC∥AC,
∴∠1=∠EPOA,
∵∠1=∠2,
∴∠2=∠C′OP,
∴OC′=PC′=11﹣x,
∴B′C′=11﹣2x,
在Rt△OB′C′中,
∵OC′2=OB′2+B′C′2,
∴62+(11﹣2x)2=(11﹣x)2,
解得x=![]() ,
,
∴AE=![]() 或
或![]() .
.
故答案为![]() 或
或![]() .
.
点睛:本题主要考查了图形的折叠问题,矩形的性质,相似三角形的判定以及运用数形结合思想列方程的综合运用,运用相似的性质列比例式得出方程求出BP是解决问题的关键.

练习册系列答案
相关题目