题目内容
【题目】若 x 满足 (9x)(x4)=4, 求 (4x)2+(x9)2 的值.
设 9x=a,x4=b, 则 (9x)(x4)=ab=4,a+b=(9x)+(x4)=5 ,
∴(9x)2+(x4)2=a2+b2=(a+b)22ab=522×4=13
请仿照上面的方法求解下面问题:
(1)若 x 满足 (5x)(x2)=2, 求 (5x)2+(x2)2 的值
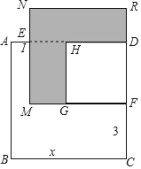
(2)已知正方形 ABCD 的边长为 x , E , F 分别是 AD 、 DC 上的点,且 AE=1 , CF=3 ,长方形 EMFD 的面积是 48 ,分别以 MF 、 DF 作正方形,求阴影部分的面积.
【答案】(1)5;(2)28
【解析】
(1)设5-x=a,x-2=b,请仿照上面的方法求解即可;
(2)根据正方形ABCD边长为x,进而表示出MF与DF,求出阴影部分面积即可.
解:(1)设 5-x=a,x-2=b,
则(5-x)(x-2)=ab=2,a+b=(5-x)+(x-2)=3,
∴(5-x) 2 +(x-2) 2 =(a+b) 2 -2ab=3 2-2×2=5;
(2)∵正方形 ABCD 的边长为 x,AE=1,CF=3,
∴MF=DE=x-1,DF=x-3,
∴(x-1)(x-3)=48,
阴影部分的面积=FM 2 -DF 2 =(x-1) 2 -(x-3) 2 .
设 x-1=a,x-3=b,则(x-1)(x-3)=ab=48,a-b=(x-1)-(x-3)=2,
∴a+b=14,
∴(x-1) 2 -(x-3) 2 =a 2 -b 2 =(a+b)(a-b)=14×2=28.
即阴影部分的面积是 28.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目