题目内容
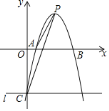
【题目】如图,抛物线y=![]() x2+mx+n与直线y=﹣
x2+mx+n与直线y=﹣![]() x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0).
x+3交于A,B两点,交x轴与D,C两点,连接AC,BC,已知A(0,3),C(3,0).
(1)求抛物线的关系式和tan∠BAC的值;
(2)P为抛物线上一动点,连接PA,过点P作PQ⊥OA交y轴于点Q,问:是否存在点P使得以A,P,Q为顶点的三角形与△ACB相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由;
(3)在AB上找一点M,使得OM+DM的值最小,直接写出点M的坐标.

【答案】(1)抛物线解析式:y=![]() x2﹣
x2﹣![]() x+3;tan∠BAC=
x+3;tan∠BAC=![]() ;(2)点P坐标为:(11,36),(
;(2)点P坐标为:(11,36),(![]() ,
,![]() ),(﹣1,6),(
),(﹣1,6),(![]() ,
,![]() );(3)M点坐标(
);(3)M点坐标(![]() ,
,![]() ).
).
【解析】
(1)C两点坐标代入二次函数的解析式,解方程组求出m、n的值即可得抛物线的解析式,利用解析式可求出D点坐标,根据抛物线和直线交于A、B两点,解方程组可求得B点坐标,根据A、B、C三点坐标可知△ABC是直角三角形,进而可求得tanBAC 的值.(2)设P(a,![]() a2﹣
a2﹣![]() a+3),根据QA=∠ACB=90°可知相似比为3或
a+3),根据QA=∠ACB=90°可知相似比为3或![]() ,分别讨论点P在点A的下方和下方两种情况,根据相似比求出a的值即可的P点坐标;(3)由A、B两点坐标求出直线AB的解析式,作点O关于直线AB的对称点O',可求出O′的坐标当O',M,D三点共线时,OM+DM值最小,连接O'D交AB于M,根据D、O′坐标可求出O'D的析式,结合AB的解析式求出M的坐标即可.
,分别讨论点P在点A的下方和下方两种情况,根据相似比求出a的值即可的P点坐标;(3)由A、B两点坐标求出直线AB的解析式,作点O关于直线AB的对称点O',可求出O′的坐标当O',M,D三点共线时,OM+DM值最小,连接O'D交AB于M,根据D、O′坐标可求出O'D的析式,结合AB的解析式求出M的坐标即可.
(1)∵抛物线y=![]() x2+mx+n过点A(0,3),点C(3,0).
x2+mx+n过点A(0,3),点C(3,0).
∴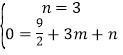 ,
,
解得:n=3,m=﹣![]() ,
,
∴抛物线解析式:y=x2﹣![]() x+3
x+3
当y=0时,0=![]() x2﹣
x2﹣![]() x+3
x+3
∴x1=3,x2=2
∴D点坐标(2,0)
∵抛物线y=![]() x2+mx+n与直线y=﹣x+3交于A,B两点
x2+mx+n与直线y=﹣x+3交于A,B两点
∴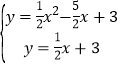 ,
,
解得:![]() ,
,![]() ;
;
∴B点坐标(4,1)
∵A(0,3),C(3,0),B(4,1)
∴AB=2![]() ,BC=
,BC=![]() ,AC=3
,AC=3![]() ,
,
∵AB2=20,BC2=2,AC2=18
∴AB2=BC2+AC2.
∴∠ACB=90°
∴tan∠BAC=![]() =
=![]() ,
,
(2)设P(a,![]() a2﹣
a2﹣![]() a+3),
a+3),
若点P在点A的下方,则PQ=a>0
∵以A,P,Q为顶点的三角形与△ACB相似,且∠PQA=∠ACB=90°
∴![]() 或
或![]() ,
,
若![]() ,则3AQ=PQ 即3[3﹣(
,则3AQ=PQ 即3[3﹣(![]() a2﹣
a2﹣![]() a+3)]=a
a+3)]=a
解得a=![]() ,a=0(不合题意舍去)
,a=0(不合题意舍去)
∴点P(![]() ,
,![]() )
)
若![]() ,则AQ=3PQ 即[3﹣(
,则AQ=3PQ 即[3﹣(![]() a2﹣
a2﹣![]() a+3)]=3a
a+3)]=3a
解得:a=0(不合题意舍去),a=﹣1(不合题意舍去)
若点P在点A上方,且在y轴左侧,则PQ=﹣a>0
∵以A,P,Q为顶点的三角形与△ACB相似,且∠PQA=∠ACB=90°
∴![]() 或
或![]()
若![]() ,则3AQ=PQ,即3[(
,则3AQ=PQ,即3[(![]() a2﹣
a2﹣![]() a+3)﹣3]=﹣a
a+3)﹣3]=﹣a
解得:a=0(不合题意舍去),a=![]() (不合题意舍去)
(不合题意舍去)
若![]() ,则AQ=3PQ 即[(
,则AQ=3PQ 即[(![]() a2﹣
a2﹣![]() a+3)﹣3]=﹣3a
a+3)﹣3]=﹣3a
解得:a=0(不合题意舍去),a=﹣1
∴点P(﹣1,6)
若点P在点A上方,且在y轴右侧,则PQ=a>0
∵以A,P,Q为顶点的三角形与△ACB相似,且∠PQA=∠ACB=90°
∴![]() 或
或![]()
若![]() ,则3AQ=PQ,即3[(
,则3AQ=PQ,即3[(![]() a2﹣
a2﹣![]() a+3)﹣3]=a
a+3)﹣3]=a
解得:a=0(不合题意舍去),a=![]() ,
,
∴点P(![]() ,
,![]() )
)
若![]() ,则AQ=3PQ 即[(
,则AQ=3PQ 即[(![]() a2﹣
a2﹣![]() a+3)﹣3]=3a
a+3)﹣3]=3a
解得:a=0(不合题意舍去),a=11,
∴点P(11,36)
综上所述:点P坐标为:(11,36),(![]() ,
,![]() ),(﹣1,6),(
),(﹣1,6),(![]() ,
,![]() )
)
(3)∵A(0,3),B(4,1)
∴直线AB的解析式:y=﹣![]() x+3
x+3
作点O关于直线AB的对称点O'(/span>![]() ,
,![]() )
)
∴OM+DM=O'M+DM
根据两点之间,线段最短,则当O',M,D三点共线时,OM+DM值最小.
连接O'D交AB于M
∵O'(![]() ,
,![]() ),D(2,0)
),D(2,0)
∴O'D解析式:y=12x﹣24
则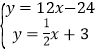
解得: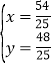
∴M点坐标(![]() ,
,![]() )
)