题目内容
【题目】综合与实践
问题情境
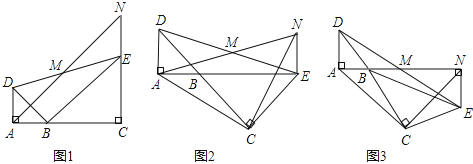
在综合与实践课上,老师组织同学们以“直角三角形的旋转”为主题开展数学活动.如图1,矩形ABCD中,AD=2AB,连接AC,将△ABC绕点A旋转到某一位置,观察图形,提出问题并加以解决.
实践操作
(1)如图2,慎思组的同学将图1中的△ABC以点A为旋转中心,按逆时针方向旋转,得到△A'B'C',此时B'C过点D,则∠ADB= 度.
(2)博学组的同学在图2的基础上继续旋转到图3,此时点C'落在CD的延长线上,连接BB',该组提出下面两个问题:
①C'D和AB有何数量关系?并说明理由.
②BB'和AC′有何位置关系?并说明理由.
请你解决该组提出的这两个问题.
提出问题
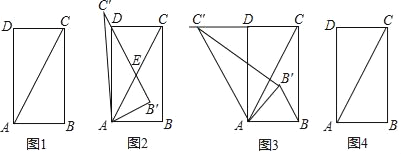
(3)请你参照以上操作,将图1中的△ABC旋转至某一位置,在图4中画出新图形,表明字母,说明构图方法,并提出一个问题,不必解答.
【答案】(1)30(2)①C′D=AB②见解析(3)见解析
【解析】
(1)由旋转性质知AB=AB′、∠B′=∠B=90°,结合AD=BC=2AB可得AD=2AB′,根据直角三角形的性质即可求解;(2)①C′D=AB,利用“HL”证Rt△ADC′≌Rt△ABC即可得;②过点C′作C′H垂直于BA延长线于点H,证△C′HA≌△C′B′A得∠HAC′=∠C′AB,由AB=AB′知∠ABB′=∠AB′B,据此根据∠HAB′=∠ABB′+∠AB′B可得2∠C′AB′=2∠AB′B,即可证得结论;(3)将△ABC以点A为旋转中心,按逆时针方向旋转得△AB′C′,AB′与对角线AC重合时,B′C′与AD交于点M,求S△AB′M:S△ADC的值?利用相似三角形的判定与性质即可解决此题.
(1)由题意知△ABC≌△AB′C′,
∴AB=AB′、∠B′=∠B=90°,
∵AD=BC=2AB,
∴在Rt△AB′D中,AD=2AB′,
则∠ADB′=30°,
故答案为:30;
(2)①C′D=AB,理由如下:
∵四边形ABCD是矩形,
∴AD=BC、∠ABC=∠ADC=∠ADC′=90°,
由旋转知AC′=AC,
在Rt△ADC′和Rt△ABC中,
∵![]() ,
,
∴Rt△ADC′≌Rt△ABC(HL),
∴C′D=AB;
②如图a,过点C′作C′H垂直于BA延长线于点H,

则四边形HADC′是矩形,
∴C′H=AD、AH=C′D=AB,
在△C′HA和△C′B′A中,
∵ ,
,
∴△C′HA≌△C′B′A(SSS),
∴∠HAC′=∠C′AB,
又∵AB=AB′,
∴∠ABB′=∠AB′B,
在△ABB′中,∠HAB′=∠ABB′+∠AB′B,即∠HAC′+∠C′AB′=∠ABB′+∠AB′B,
∴2∠C′AB′=2∠AB′B,
∴∠C′AB′=∠AB′B,
∴AC′∥BB′;
(3)如图b,
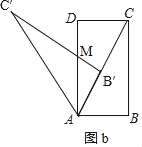
将△ABC以点A为旋转中心,按逆时针方向旋转得△AB′C′,AB′与对角线AC重合时,B′C′与AD交于点M,求S△AB′M:S△ADC的值?

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案