题目内容
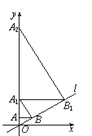
【题目】如图,直线y1=kx+2与反比例函数y2= ![]() 的图象交于点A(m,3),与坐标轴分别交于B,C两点.
的图象交于点A(m,3),与坐标轴分别交于B,C两点.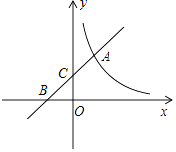
(1)若y1>y2>0,求自变量x的取值范围;
(2)动点P(n,0)在x轴上运动,当n为何值时,|PA﹣PC|的值最大?并求最大值.
【答案】
(1)解:当y2= ![]() =3时,x=1,
=3时,x=1,
∴点A的坐标为(1,3).
观察函数图象,可知:当x>1时,直线在双曲线上方,
∴若y1>y2>0,自变量x的取值范围为x>1.
(2)解:将A(1,3)代入y1=kx+2中,
3=k+2,解得:k=1,
∴直线AB的解析式为y1=x+2.
当x=0时,y1=x+2=2,
∴点C的坐标为(0,2),
∴AC= ![]() =
= ![]() .
.
当y1=x+2=0时,x=﹣2,
∴点B的坐标为(﹣2,0).
当点P于点B重合时,|PA﹣PC|的值最大,此时n=﹣2,|PA﹣PC|=AC= ![]() .
.
∴当n为﹣2时,|PA﹣PC|的值最大,最大值为 ![]() .
.
【解析】(1)把点A(m,3),代入反比例函数的解析式,求出m的值,观察函数图象,可知当x>1时,直线在双曲线上方,求出自变量x的取值范围即可;(2)将A(1,3)代入直线解析式,求出直线AB的解析式,得到点C的坐标,根据两点间的距离求出AC的值,得到点B的坐标,求出|PA﹣PC|的最大值.

练习册系列答案
相关题目