题目内容
【题目】如图，二次函数的图象与x轴相交于点A（﹣3，0）、B（﹣1，0），与y轴相交于点C（0，3），点P是该图象上的动点；一次函数y=kx﹣4k（k≠0）的图象过点P交x轴于点Q．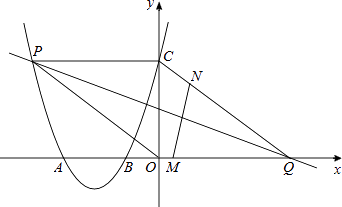
（1）求该二次函数的解析式；
（2）当点P的坐标为（﹣4，m）时，求证：∠OPC=∠AQC；
（3）点M，N分别在线段AQ、CQ上，点M以每秒3个单位长度的速度从点A向点Q运动，同时，点N以每秒1个单位长度的速度从点C向点Q运动，当点M，N中有一点到达Q点时，两点同时停止运动，设运动时间为t秒．
①连接AN，当△AMN的面积最大时，求t的值；
②直线PQ能否垂直平分线段MN？若能，请求出此时点P的坐标；若不能，请说明你的理由．
【答案】
（1）
解：设抛物线的解析式为：y=a（x+3）（x+1），
∵抛物线经过点C（0，3），
∴3=a×3×1，解得a=1．
∴抛物线的解析式为：y=（x+3）（x+1）=x2+4x+3
（2）
证明：在抛物线解析式y=x2+4x+3中，当x=﹣4时，y=3，∴P（﹣4，3）．
∵P（﹣4，3），C（0，3），
∴PC=4，PC∥x轴．
∵一次函数y=kx﹣4k（k≠0）的图象交x轴于点Q，当y=0时，x=4，
∴Q（4，0），OQ=4．
∴PC=OQ，又∵PC∥x轴，
∴四边形POQC是平行四边形，
∴∠OPC=∠AQC
（3）
解：①在Rt△COQ中，OC=3，OQ=4，由勾股定理得：CQ=5．
如答图1所示，过点N作ND⊥x轴于点D，则ND∥OC，
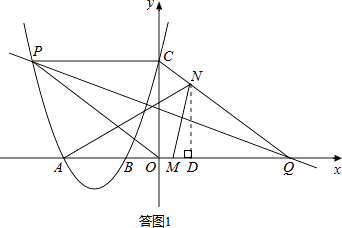
∴△QND∽△QCO，
∴ 
，即 
，解得：ND=3﹣ 
t．
设S=S△AMN，则：
S= 
AMND= 3t（3﹣ t）=﹣ 
（t﹣ 
）2+ 
．
又∵AQ=7，∴点M到达终点的时间为t= 
，
∴S=﹣ （t﹣ ）2+ （0＜t≤ ）．
∵﹣ ＜0， ＜ ，且x＜ 时，y随x的增大而增大，
t=2.5时已超过运动时间又因为开口向下所以取 ，
∴当t= 时，△AMN的面积最大．
②假设直线PQ能够垂直平分线段MN，则有QM=QN，且PQ⊥MN，PQ平分∠AQC．
由QM=QN，得：7﹣3t=5﹣t，解得t=1．
设P（x，x2+4x+3），
若直线PQ⊥MN，则：过P作直线PE⊥x轴，垂足为E，
则△PEQ∽△MDN，
∴ 
，
∴ 
∴x= 
，
∴P（ 
， 
）或（ 
， 
）
∴直线PQ能垂直平分线段MN
【解析】（1）利用交点式求出抛物线的解析式；（2）证明四边形POQC是平行四边形，则结论得证；（3）①求出△AMN面积的表达式，利用二次函数的性质，求出△AMN面积最大时t的值．注意：由于自变量取值范围的限制，二次函数并不是在对称轴处取得最大值；②直线PQ上的点到∠AQC两边的距离相等，则直线PQ能平分∠AQC，所以直线PQ能垂直平分线段MN．
