题目内容
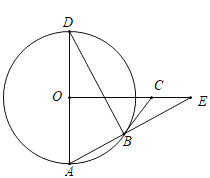
【题目】如图,![]() 是
是![]() 的直径,弦
的直径,弦![]() 点
点![]() 是直径
是直径![]() 上方半圆上的动点(包括端点
上方半圆上的动点(包括端点![]() 和
和![]() 的平分线相交于点E,当点
的平分线相交于点E,当点![]() 从点
从点![]() 运动到点
运动到点![]() 时,则
时,则![]() 两点的运动路径长的比值是( )
两点的运动路径长的比值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
延长![]() 交
交![]() 于点
于点![]() ,连接DA、DB,由圆周角定理和等角对等边的性质可知DA=DE,据此可知,
,连接DA、DB,由圆周角定理和等角对等边的性质可知DA=DE,据此可知,![]() 在以
在以![]() 为圆心,
为圆心,![]() 长为半径的圆上,根据角平分线的性质、圆周角定理及等边三角形的判定可知
长为半径的圆上,根据角平分线的性质、圆周角定理及等边三角形的判定可知![]() 为等边三角形,进而可知DA=DB=DO,由此可知,当
为等边三角形,进而可知DA=DB=DO,由此可知,当![]() 由
由![]() 运动到到
运动到到![]() 时,
时,![]() 运动路径为
运动路径为![]() ,
,![]() 运动路径为
运动路径为![]() ,与
,与![]() 对应的圆周半径相同,最后计算路径长度比即为圆心角之比.
对应的圆周半径相同,最后计算路径长度比即为圆心角之比.
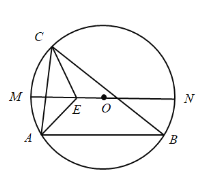
如图1,延长![]() 交
交![]() 于点
于点![]() ,
,
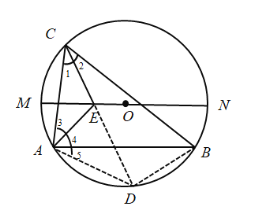
由![]() 平分
平分![]() 得
得![]() 恒为劣弧
恒为劣弧![]() 中点.
中点.
由已知,得![]() ,
,
则![]() ,
,
得![]() .
.
故![]() 在以
在以![]() 为圆心,
为圆心,![]() 长为半径的圆上.
长为半径的圆上.
∵∠ACB=2∠2=60°,
∴∠2=30°,
∴∠BOD=60°,
∵DO=BO,
∴△BOD是等边三角形,
∴DO=DB=DA,
如图2,当![]() 由
由![]() 运动到到
运动到到![]() 时,
时,![]() 运动轨迹为
运动轨迹为![]() .
.
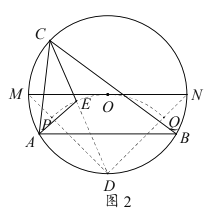
![]() 运动路径为
运动路径为![]() 与路径
与路径![]() 对应的圆周半径相同,计算路径长度比即为圆心角之比,
对应的圆周半径相同,计算路径长度比即为圆心角之比,
由![]() 得路径长度之比为
得路径长度之比为![]() .
.
故选:C.

练习册系列答案
相关题目
【题目】某市一研究机构为了了解![]() 岁年龄段市民对创建文明城市的关注程度,随机选取了
岁年龄段市民对创建文明城市的关注程度,随机选取了![]() 名年龄在该范围内的市民进行了调查,并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
名年龄在该范围内的市民进行了调查,并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
组别 | 年龄段 | 频数(人数) |
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
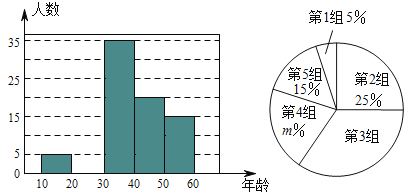
(1)请直接写出![]() ,第
,第![]() 组人数在扇形统计图中所对应的圆心角是 度;
组人数在扇形统计图中所对应的圆心角是 度;
(2)请补全上面的频数分布直方图:
(3)假设该市现有![]() 岁的市民
岁的市民![]() 万人,问
万人,问![]() 岁年龄段的关注创建文明城市的人数约有多少?
岁年龄段的关注创建文明城市的人数约有多少?