题目内容
【题目】现有
，
两个不透明的袋子，分别装有3个除颜色外完全相同的小球．其中，袋装有1个白球，2个红球；袋装有1个红球，2个白球．
（1）将袋摇匀，然后从袋中随机摸出一个球，则摸出的小球是红球的概率为______；
（2）小王和小周商定了一个游戏规则：从摇匀后的，两袋中各随机摸出一个球，摸出的这两个球，若颜色相同，则小王获胜；若颜色不同，则小周获胜．请利用概率说明这个游戏规则是否公平．
【答案】（1）
；（2）这个游戏规则是不公平．
【解析】
（1）用A袋中红球个数÷A袋中总球数即可；
（2）（2）由上表可知，共有9种等可能结果，其中颜色不相同的结果有4种，颜色相同的结果有5种，则P（颜色不相同）
，P（颜色相同）
，因此这个游戏规则对双方不公平．
解：（1）共有3种等可能结果，而摸出红球的结果有2种，
∴P（摸出红球）
；
（2）根据题意，画出树状图：
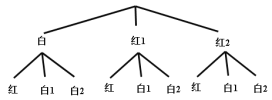
由树状图可以看出，所有可能出现的结果有9种，并且它们出现的可能性相等，其中颜色相同的结果有4种，颜色不同的结果有5种．
所以
（颜色相同）；（颜色不同）．
∵
，
∴这个游戏规则是不公平．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
