题目内容
【题目】已知:在△ABC中,∠ACB=90°,点P是线段AC上一点,过点A作AB的垂线,交BP的延长线于点M,MN⊥AC于点N,PQ⊥AB于点Q,AQ=MN. 求证:
(1)△APM是等腰三角形;
(2)PC=AN.

【答案】(1)见解析;(2)见解析
【解析】
(1)利用条件得到∠BAM=∠ANM=90°,∠PAQ=∠AMN即可解答.
(2)转换角度,利用角平分线性质解答.
(1)解:∵BA⊥AM,MN⊥AC,
∴∠BAM=∠ANM=90°,
∴∠PAQ+∠MAN=∠MAN+∠AMN=90°,
∴∠PAQ=∠AMN,
∵PQ⊥AB,MN⊥AC,
∴∠PQA=∠ANM=90°,
在△AQP和△MNA中,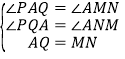
∴△AQP≌△MNA,
∴MA=AP,
∴△APM是等腰三角形.
(2)解:∵MA=AP,
∴∠AMP=∠APM,
∵∠APM=∠BPC,
∴∠AMP=∠BPC,
∵∠BPC+∠PBC=90°,∠AMB+∠ABM=180°-∠BAM=90°,
∴∠ABM=∠PBC,
∵PQ⊥AB,PC⊥BC,
∴PQ=PC(角平分线的性质),
由(1)可知AN=PQ,
∴PC=AN.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某篮球队要从小军和小勇两名队员中选派一人参加市篮球协会的投篮比赛,在最近的十次选拔测试中,他俩投篮十次的进球个数如下表所示:
小军 | 7 | 8 | 8 | 8 | 8 | 9 | 8 | 9 | 7 | 8 |
小勇 | 7 | 8 | 9 | 5 | 9 | 10 | 7 | 10 | 9 | 6 |
(l)请填写下表:
平均数 | 中位数 | 众数 | 极差 | 方差 | |
小军 | 8 | 8 | ______ | span>2 | ______ |
小勇 | ______ | ______ | 9 | _______ | 2.6 |
(2)历届比赛成绩表明,十次投进八球就很可能获奖但很难夺冠,十次投进九球就很可能夺冠,那么你认为想要获奖应该派谁参赛,想要夺冠应该派谁参赛?请说明理由.




