题目内容
【题目】如图，在梯形ABCD中，已知AD∥BC，AB=CD，延长线段CB到E，使BE=AD，连接AE、AC.
【1】求证：△ABE≌△CDA；
【2】若∠DAC=40°，求∠EAC的度数.
【答案】
【1】见解析
【2】100°
【解析】⑴利用SAS求证△ABE≌△CDA
⑵利用△ABE≌△CDA和平行线的性质以及等腰三角形的性质求解
⑴证明：在梯形ABCD中，∵AD∥BC，AB=CD，
∴∠ABE=∠BAD，∠BAD=∠CDA.
∴∠ABE=∠CDA.
在△ABE和△CDA中，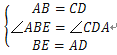
∴△ABE≌△CDA.
⑵解：由⑴得：∠AEB=∠CAD，AE=AC.
∴∠AEB=∠ACE.
]∵∠DAC=40°∴∠AEB=∠ACE=40°.
∴∠EAC=180°－40°－40°=100°.
阅读快车系列答案
【题目】为了美化学习环境，加强校园绿化建设，某校计划用不多于5200元的资金购买A、B两种树苗共60棵（可以是同一种树苗），加强校园绿化建设．若购买A种树苗x棵，所需总资金为y元，A、B两种树苗的相关信息如表：
项目 | 单价（元/棵） | 成活率 |
A | 100 | 98% |
B | 60 | 90% |
（1）求y与x之间的函数关系式；
（2）若要使得所购买树苗的成活率不低于95%，有几种选购方案？所用的资金分别是多少？
【题目】为了解饮料自动售货机的销售情况，有关部门从北京市所有的饮料自动售货机中随机抽取20台进行了抽样调查，记录下某一天各自的销售情况
单位：元
，并对销售金额进行分组，整理成如下统计表：
28，8，18，63，15，30，70，42，36，47，
25，58，64，58，55，41，58，65，72，30
销售金额x |
|
|
|
|
划记 |
|
| ______ | ______ |
频数 | 3 | 5 | ______ | ______ |
请将表格补充完整；
用频数分布直方图将20台自动售货机的销售情况表示出来，并在图中标明相应数据；
根据绘制的频数分布直方图，你能获取哪些信息？至少写出两条不同类型信息
