题目内容
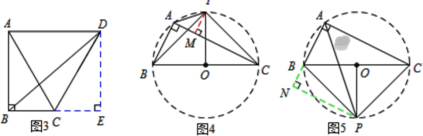
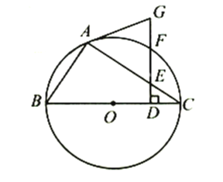
【题目】如图,![]() 为⊙
为⊙![]() 的内接三角形,
的内接三角形,![]() 为⊙
为⊙![]() 的直径,在线段
的直径,在线段![]() 上取点
上取点![]() (不与端点重合),作
(不与端点重合),作![]() ,分别交
,分别交![]() 、圆周于
、圆周于![]() 、
、![]() ,连接
,连接![]() ,已知
,已知![]() .
.
(1)求证:![]() 为⊙
为⊙![]() 的切线;
的切线;
(2)已知![]() ,填空:
,填空:
①当![]() __________
__________![]() 时,四边形
时,四边形![]() 是菱形;
是菱形;
②若![]() ,当
,当![]() __________时,
__________时,![]() 为等腰直角三角形.
为等腰直角三角形.
【答案】(1)证明见解析;(2)①![]() ;②
;②![]() .
.
【解析】
(1)连接![]() ,利用已知条件和圆的基本性质证明
,利用已知条件和圆的基本性质证明![]() 即可得到直线AG是⊙O的切线;
即可得到直线AG是⊙O的切线;
(2)①假设四边形![]() 为菱形,易得△AOB为等边三角形,可得∠ABC=120°,可得
为菱形,易得△AOB为等边三角形,可得∠ABC=120°,可得![]() ,即可得出答案;
,即可得出答案;
②假设![]() 为等腰直角三角形,可得
为等腰直角三角形,可得![]() ,可得:
,可得:![]() 和
和![]() 都是等腰三角形,可证:四边形
都是等腰三角形,可证:四边形![]() 为矩形,由
为矩形,由![]() ,可得
,可得![]() ,可证
,可证![]() ,计算可得
,计算可得![]() ,即可得出答案.
,即可得出答案.
证明:(1)如图,连接![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
即![]()
![]() 为半径,
为半径,
![]() 为⊙
为⊙![]() 的切线;
的切线;
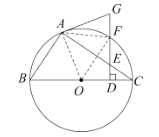
(2)答案为:![]() ;
;![]() .提示如下:
.提示如下:
①若四边形![]() 为菱形,
为菱形,
![]() ,
,
又![]() ,
,
![]() 为等边三角形,
为等边三角形,
![]() ,
,
![]() ,
,
![]() ;
;
②如图所示,若![]() 为等腰直角三角形,
为等腰直角三角形,
![]() ,
,
![]() 和
和![]() 都是等腰三角形,在等腰
都是等腰三角形,在等腰![]() 中,
中,![]() 为斜边中线,
为斜边中线,
![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 为矩形,
为矩形,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() .
.
故答案为:![]() ;
;![]() .
.


练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目