Question

【题目】垦利区在进行“五城同创”的过程中，决定购买A，B两种树对某路段进行绿化改造，若购买A种树1棵，B种树3棵，需要2250元；购买A种树2棵，B种树5棵，需要3900元．

（1）求购买A，B两种树每棵各需多少元？

（2）考虑到绿化效果，购进A种树不能少于48棵，且用于购买这两种树的资金不低于52500元．若购进这两种树共100棵．问有哪几种购买方案？

Answer 1

【答案】（1）购买A种树每棵需要450元，B种树每棵需要600元；（2）有三种购买方案：A种树购买48棵，B种树购买52棵；A种树购买49棵，B种树购买51棵；A种树购买50棵，B种树购买50棵

【解析】

（1）本题有两个相等关系：购买1棵A种树的钱数+3棵B种树的钱数=2250元；购买2棵A种树的钱数+5棵B种树的钱数=3900元，据此设未知数列方程组解答即可；

（2）设购进A种树m棵，根据购进A种树不能少于48棵，且用于购买这两种树的资金不低于52500元即可列出关于m的不等式组，解不等式组即可求出m的取值范围，然后结合m为整数即可得出结论．

解：（1）设购买A种树每棵需要x元，B种树每棵需要y元，

依题意，得：， 解得：．

答：购买A种树每棵需要450元，B种树每棵需要600元．

（2）设购进A种树m棵，则购进B种树（100﹣m）棵，

依题意，得：，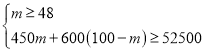

解得：48≤m≤50．

∵m为整数，∴m为48，49，50．

当m＝48时，100﹣m＝100﹣48＝52；

当m＝49时，100﹣m＝100﹣49＝51；

当m＝50时，100﹣m＝100﹣50＝50．

答：有三种购买方案：A种树购买48棵，B种树购买52棵；A种树购买49棵，B种树购买51棵；A种树购买50棵，B种树购买50棵．