题目内容
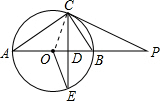
如图,AB是⊙O的直径,点P在AB的延长线上,弦CE交AB于点D.连接OE、AC,已知∠POE=2∠ CAB,∠P=∠E.
CAB,∠P=∠E.
(1)求证:CE⊥AB;
(2)求证:PC是⊙O的切线;
(3)若BD=20D,PB=9,求⊙O的半径及tan∠P的值.
 CAB,∠P=∠E.
CAB,∠P=∠E.(1)求证:CE⊥AB;
(2)求证:PC是⊙O的切线;
(3)若BD=20D,PB=9,求⊙O的半径及tan∠P的值.
(1)证明:连接OC,
∴∠COB=2∠CAB,
又∠POE=2∠CAB.
∴∠COD=∠EOD,
又∵OC=OE,
∴∠ODC=∠ODE=90°,
即CE⊥AB;
(2)证明:∵CE⊥AB,∠P=∠E,
∴∠P+∠PCD=∠E+∠PCD=90°,
又∠OCD=∠E,
∴∠OCD+∠PCD=∠PCO=90°,
∴PC是⊙O的切线;
(3)设⊙O的半径为r,OD=x,则BD=2x,r=3x,
∵CD⊥OP,OC⊥PC,
∴Rt△OCD∽Rt△OPC,
∴OC2=OD•OP,即(3x)2=x•(3x+9),
解之得x=
,
∴⊙O的半径r=
,
同理可得PC2=PD•PO=(PB+BD)•(PB+OB)=162,
∴PC=9
,
在Rt△OCP中,tan∠P=
=
.
∴∠COB=2∠CAB,
又∠POE=2∠CAB.
∴∠COD=∠EOD,
又∵OC=OE,
∴∠ODC=∠ODE=90°,
即CE⊥AB;
(2)证明:∵CE⊥AB,∠P=∠E,
∴∠P+∠PCD=∠E+∠PCD=90°,
又∠OCD=∠E,
∴∠OCD+∠PCD=∠PCO=90°,
∴PC是⊙O的切线;
(3)设⊙O的半径为r,OD=x,则BD=2x,r=3x,
∵CD⊥OP,OC⊥PC,
∴Rt△OCD∽Rt△OPC,
∴OC2=OD•OP,即(3x)2=x•(3x+9),
解之得x=
| 3 |
| 2 |
∴⊙O的半径r=
| 9 |
| 2 |
同理可得PC2=PD•PO=(PB+BD)•(PB+OB)=162,
∴PC=9
| 2 |
在Rt△OCP中,tan∠P=
| OC |
| PC |
| ||
| 4 |


练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目


 .
. 且与BC所在直线相交?
且与BC所在直线相交?