题目内容
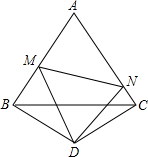
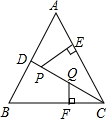
如图,过等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,且PA=CQ,连PQ交AC边于D.
(1)求证:PD=DQ;
(2)若△ABC的边长为1,求DE的长.
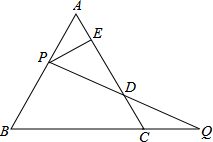
(1)求证:PD=DQ;
(2)若△ABC的边长为1,求DE的长.

(1)证明:
如图,
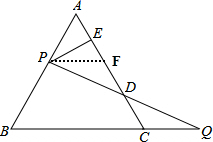
过P做PF∥BC交AC于点F,
∴∠AFP=∠ACB,∠FPD=∠Q,∠PFD=∠QCD
∵△ABC为等边三角形,
∴∠A=∠ACB=60°,
∴∠A=∠AFP=60°,
∴△APF是等边三角形;
∵AP=PF,AP=CQ,
∴PF=CQ
∴△PFD≌△QCD,
∴PD=DQ.
(2)△APF是等边三角形,
∵PE⊥AC,
∴AE=EF,
△PFD≌△QCD,
∴CD=DF,
DE=EF+DF=
AC,
∵AC=1,
DE=
.
如图,

过P做PF∥BC交AC于点F,
∴∠AFP=∠ACB,∠FPD=∠Q,∠PFD=∠QCD
∵△ABC为等边三角形,
∴∠A=∠ACB=60°,
∴∠A=∠AFP=60°,
∴△APF是等边三角形;
∵AP=PF,AP=CQ,
∴PF=CQ
∴△PFD≌△QCD,
∴PD=DQ.
(2)△APF是等边三角形,
∵PE⊥AC,
∴AE=EF,
△PFD≌△QCD,
∴CD=DF,
DE=EF+DF=
| 1 |
| 2 |
∵AC=1,
DE=
| 1 |
| 2 |

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目