题目内容
 如图,已知Rt△ABC中,∠ABC=90°,∠CAB=30°,BC=5.过点A作AE⊥AB,且AE=15,连接BE交AC于点P.
如图,已知Rt△ABC中,∠ABC=90°,∠CAB=30°,BC=5.过点A作AE⊥AB,且AE=15,连接BE交AC于点P.(1)求BE的长;
(2)以点A为圆心,AP为半径作⊙A,试判断BE与⊙A是否相切,并说明理由.
分析:由三角函数求得AB的长,再根据勾股定理即可求得BE的长;
由已知可证明得到∠APE=90°,即BE与⊙A相切.
由已知可证明得到∠APE=90°,即BE与⊙A相切.
解答: 解:(1)∵∠ABC=90°,∠CAB=30°,
解:(1)∵∠ABC=90°,∠CAB=30°,
∴AB=
=5
.(2分)
∵∠EAB=90°,AE=15,
∴BE=
=10
.(负值已舍去).(3分)
(2)BE与⊙A是相切.(4分)
∵∠EAB=90°,AE=15,AB=5
.
∴tan∠E=
=
,
∴∠E=30°.(5分)
∵∠EAB=90°,∠CAB=30°,
∴∠EAP=60°,
∴∠APE=180°-60°-30°=90°,(6分)
∴BE与⊙A是相切.(7分)
 解:(1)∵∠ABC=90°,∠CAB=30°,
解:(1)∵∠ABC=90°,∠CAB=30°,∴AB=
| BC |
| tan∠CAB |
| 3 |
∵∠EAB=90°,AE=15,
∴BE=
| AB2+AE2 |
| 3 |
(2)BE与⊙A是相切.(4分)
∵∠EAB=90°,AE=15,AB=5
| 3 |
∴tan∠E=
| AB |
| AE |
| ||
| 3 |
∴∠E=30°.(5分)
∵∠EAB=90°,∠CAB=30°,
∴∠EAP=60°,
∴∠APE=180°-60°-30°=90°,(6分)
∴BE与⊙A是相切.(7分)
点评:本题考查的是切线的判定.要证某线是圆的切线,已知此线过圆上某点,连接圆心和这点(即为半径),再证垂直即可.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 22、如图,已知Rt△ABC,AB=AC,∠ABC的平分线BD交AC于点D,BD的垂直平分线分别交AB,BC于点E、F,CD=CG.
22、如图,已知Rt△ABC,AB=AC,∠ABC的平分线BD交AC于点D,BD的垂直平分线分别交AB,BC于点E、F,CD=CG.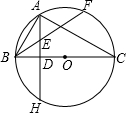 E,交⊙O于点F,且AE=BE.
E,交⊙O于点F,且AE=BE.
 5、如图,已知Rt△ABC中,∠BAC=90°,AB=AC,P是BC延长线上一点,PE⊥AB交BA延长线于E,PF⊥AC交AC延长线于F,D为BC中点,连接DE,DF.求证:DE=DF.
5、如图,已知Rt△ABC中,∠BAC=90°,AB=AC,P是BC延长线上一点,PE⊥AB交BA延长线于E,PF⊥AC交AC延长线于F,D为BC中点,连接DE,DF.求证:DE=DF. 如图,已知Rt△ABC中∠A=90°,AB=3,AC=4.将其沿边AB向右平移2个单位得到△FGE,则四边形ACEG的面积为
如图,已知Rt△ABC中∠A=90°,AB=3,AC=4.将其沿边AB向右平移2个单位得到△FGE,则四边形ACEG的面积为