题目内容
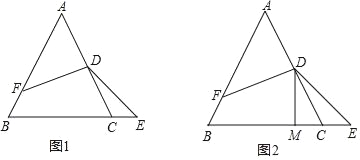
【题目】如图1,等边△ABC中,D为AC中点,∠EDF=120°,DF交AB于F点,且AF=nBF(n为常数,且n>1).
(1)求证:DF=DE;
(2)如图1,求证:AF﹣CE=![]() AB;
AB;
(3)如图2,当n= 时,过D作DM⊥BC于M点,C为EM的中点.
【答案】(1)见解析;(2)见解析;(3)3.
【解析】
(1)过D点作DG∥BC交AB于G点,证明△DGF≌△DCE,根据全等三角形的性质证明即可;
(2)根据全等三角形的性质得到GF=CE,结合图形证明;
(3)根据直角三角形的性质得到CM=![]() CD,得到GF=
CD,得到GF=![]() AG,根据等边三角形的性质解答.
AG,根据等边三角形的性质解答.
解:(1)证明:过D点作DG∥BC交AB于G点,
∵DG∥BC,
∴∠ADG=∠ACB=60°=∠A,
∴△AGD为等边三角形,
∴GD=AD=DC,
∵∠GDC=∠FDE=120°,
∴∠GDF=∠DCE,
在△DGF和△DCE中,
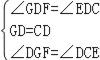
∴△DGF≌△DCE(ASA)
∴DF=DE;
(2)∵△DGF≌△DCE,
∴GF=CE,
∵DG∥BC,D为AC中点,
∴AG=![]() AB,
AB,
∴AF﹣CE=AF﹣GF=AG=![]() AB;
AB;
(3)∵DM⊥BC,∠DCM=60°,
∴CM=![]() CD,
CD,
∵C为EM的中点,
∴CE=![]() CD,
CD,
由(1)得,CE=GF,
∴GF=![]() CD,
CD,
∴GF=![]() AG=
AG=![]() GB,
GB,
∴AF=3BF,
∴n=3,
故答案为:3.

练习册系列答案
相关题目