题目内容
【题目】如图,抛物线y=x2﹣4x与x轴交于O,A两点,P为抛物线上一点,过点P的直线y=x+m与对称轴交于点Q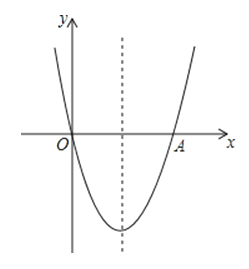
(1)这条抛物线的对称轴是 ,直线PQ与x轴所夹锐角的度数是 .
(2)若两个三角形面积满足S△POQ=![]() S△PAQ , 求m的值
S△PAQ , 求m的值
(3)当点P在x轴下方的抛物线上时,过点C(2,2)的直线AC与直线PQ交于点D,求:①PD+DQ的最大值;②PDDQ的最大值.
【答案】
(1)2;![]()
(2)
设直线PQ交x轴于点B,分别过O点,A点作PQ的垂线,垂足分别是E、F,显然当点B在OA的延长线时,S△POQ=![]() S△PAQ不成立;
S△PAQ不成立;
①当点B落在线段OA上时,如图①,

![]() =
=![]() =
=![]() ,
,
由△OBE∽△ABF得,![]() =
=![]() =
=![]() ,
,
∴AB=3OB,
∴OB=![]() OA,
OA,
由y=x2﹣4x得点A(4,0),
∴OB=1,
∴B(1,0),
∴1+m=0,
∴m=﹣1;
②当点B落在线段AO的延长线上时,如图②,
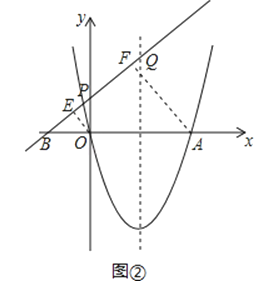
同理可得OB=![]() OA=2,
OA=2,
∴B(﹣2,0),
∴﹣2+m=0,
∴m=2,
综上,当m=﹣1或2时,S△POQ=![]() S△PAQ;
S△PAQ;
(3)
①过点C作CH∥x轴交直线PQ于点H,如图③,
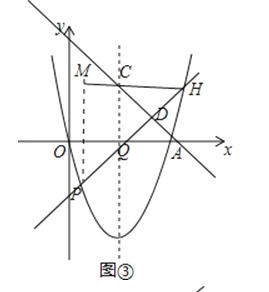
可得△CHQ是等腰三角形,
∵∠CDQ=45°+45°=90°,
∴AD⊥PH,
∴DQ=DH,
∴PD+DQ=PH,
过P点作PM⊥CH于点M,则△PMH是等腰直角三角形,
∴PH=![]() PM,
PM,
∴当PM最大时,PH最大,
∴当点P在抛物线顶点出时,PM最大,此时PM=6,
∴PH的最大值为![]() ,
,
即PD+DQ的最大值为![]() .
.
②由①可知:PD+DQ≤![]() ,
,
设PD=a,则DQ![]() ﹣a,
﹣a,
∴PDDQ≤a(![]() ﹣a)=﹣a2+
﹣a)=﹣a2+![]() a=﹣(a﹣
a=﹣(a﹣![]() )2+18,
)2+18,
∵当点P在抛物线的顶点时,a=![]() ,
,
∴PDDQ≤18.
∴PDDQ的最大值为18.
【解析】解:(1)∵y=x2﹣4x=(x﹣2)2﹣4,
∴抛物线的对称轴是x=2,
∵直线y=x+m,
∴直线与坐标轴的交点坐标为(﹣m,0),(0,m),
∴交点到原点的距离相等,
∴直线与坐标轴围成的三角形是等腰直角三角形,
∴直线PQ与x轴所夹锐角的度数是45°,
故答案为x=2、45°.
(1)把抛物线的解析式化成顶点式即可求得对称轴;求得直线与坐标轴的交点坐标,即可证得直线和坐标轴围成的图形是等腰直角三角形,从而求得直线PQ与x轴所夹锐角的度数;
(2)分三种情况分别讨论根据已知条件,通过△OBE∽△ABF对应边成比例即可求得;
(3)①过点C作CH∥x轴交直线PQ于点H,可得△CHQ是等腰三角形,进而得出AD⊥PH,得出DQ=DH,从而得出PD+DQ=PH,过P点作PM⊥CH于点M,则△PMH是等腰直角三角形,得出PH=![]() PM,因为当PM最大时,PH最大,通过求得PM的最大值,从而求得PH的最大值;由①可知:PD+PH≤6
PM,因为当PM最大时,PH最大,通过求得PM的最大值,从而求得PH的最大值;由①可知:PD+PH≤6![]() ,设PD=a,则DQ
,设PD=a,则DQ![]() ﹣a,得出PDDQ≤a(6
﹣a,得出PDDQ≤a(6![]() ﹣a)=﹣a2+6
﹣a)=﹣a2+6![]() a=﹣(a﹣3
a=﹣(a﹣3![]() )2+18,当点P在抛物线的顶点时,a=3
)2+18,当点P在抛物线的顶点时,a=3![]() ,得出PDDQ≤18.
,得出PDDQ≤18.