题目内容
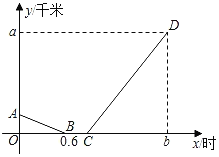
【题目】小明星期天上午8:00从家出发到离家36千米的书城买书,他先从家出发骑公共自行车到公交车站,等了12分钟的车,然后乘公交车于9:48分到达书城(假设在整个过程中小明骑车的速度不变,公交车匀速行驶,小明家、公交车站、书城依次在一条笔直的公路旁).如图是小明从家出发离公交车站的路程y(千米)与他从家出发的时间x(时)之间的函数图象,其中线段AB对应的函教表达式为y=kx+6.
(1)求小明骑公共自行车的速度;
(2)求线段CD对应的函数表达式;
(3)求出发时间x在什么范围时,小明离公交车站的路程不超过3千米?
【答案】(1)10千米/小时;(2)y=30x﹣24;(3)0.3≤x≤0.9
【解析】
(1)根据线段AB对应的函教表达式为y=kx+6和函数图象中的数据,可以求得k的值,然后即可得到点A的坐标,从而可以求得小明骑公共自行车的速度;
(2)根据题意,可以得到点C和点D的坐标,然后即可求得线段CD对应的函数表达式;
(3)根据前面求出的函数解析式,可以得到出发时间x在什么范围时,小明离公交车站的路程不超过3千米.
解:(1)∵线段AB对应的函教表达式为y=kx+6,点(0.6,0)在y=kx+6上,
∴0=0.6k+6,得k=﹣10,
∴y=﹣10x+6,
当x=0时,y=6,
∴小明骑公共自行车的速度为6÷0.6=10(千米/小时),
答:小明骑公共自行车的速度是10千米/小时;
(2)∵点C的横坐标为:0.6+![]() =0.8,
=0.8,
∴点C的坐标为(0.8,0),
∵从8:00到9:48分是1.8小时,点D的纵坐标是36﹣6=30,
∴点D的坐标为(1.8,30),
设线段CD对应的函数表达式是y=mx+n,
![]() ,得
,得![]() ,
,
即线段CD对应的函数表达式是y=30x﹣24;
(3)令﹣10x+6≤3,得x≥0.3,
令30x﹣24≤3,得x≤0.9,
即出发时间x在0.3≤x≤0.9范围时,小明离公交车站的路程不超过3千米.

 名校课堂系列答案
名校课堂系列答案