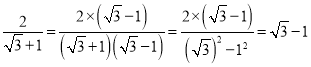题目内容
【题目】如图,点A、B分别是x轴、y轴上的点,点A的坐标为(a,0),点B的坐标为(0,b),点M坐标为(1,1)
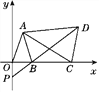
(1)如图1中的第一象限内,若a=2,b=1,画出线段AB关于点M(1,1)的中心对称线段CD,并写出C、D两点的坐标;
(2)如图,若AB关于M(1,1)中心对称的线段为CD,点C、点D在双曲线y=![]() (x>0)上,且AB=
(x>0)上,且AB=![]() ,求k的值;
,求k的值;
(3)若a=![]() ,b=
,b=![]() ,直接写出直线CD的解析式.
,直接写出直线CD的解析式.

【答案】(1)C(0,1),D(2,1);(2)k=2;(3)y=﹣x+![]() .
.
【解析】
(1)如图1中,设C(m,n),D(p,q).利用中点坐标公式计算即可;
(2)如图2中,由题意点C的纵坐标为2,点D的横坐标为2,由点C、D在反比例函数y=![]() 上,可以假设C(m,2),D(2,m),根据AB=CD=
上,可以假设C(m,2),D(2,m),根据AB=CD=![]() ,2-m=1,可得m=1,求出点D坐标即可解决问题;
,2-m=1,可得m=1,求出点D坐标即可解决问题;
(3)设C(m,n),D(p,q).利用中点坐标公式求出C、D两点坐标,再利用待定系数法即可解决问题;
解:(1)如图1中,设C(m,n),D(p,q).

由题意A(2,0),B(0,1),
∵A、C关于M对称,B、D关于M对称,
∴![]() =1,
=1,![]() =1,
=1,![]() =1,
=1,![]() =1,
=1,
解得m=0,n=2,p=2,q=1,
∴C(0,1),D(2,1).
(2)如图2中,由题意点C的纵坐标为2,点D的横坐标为2,

∵点C、D在反比例函数y=![]() 上,
上,
∴可以假设C(m,2),D(2,m),
∵AB=CD=![]() ,
,
∴2﹣m=1,
∴m=1,
∴C(1,2),D(2,1),
把C(1,2)代入y=![]() 中,得到k=2.
中,得到k=2.
(3)设C(m,n),D(p,q).由题意A(![]() ,0),B(0,
,0),B(0,![]() ),
),
∵A、C关于M对称,B、D关于M对称,
∴![]() =1,
=1,![]() =1,
=1,![]() =1,
=1,![]() =1,
=1,
解得m=![]() ,n=2,p=2,q=
,n=2,p=2,q=![]() ,
,
∴C(![]() ,2),D(2,
,2),D(2,![]() ),设直线CD的解析式为y=kx+b,
),设直线CD的解析式为y=kx+b,
则有 ,解得
,解得 ,
,
∴直线CD的解析式为y=﹣x+![]() .
.

 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案