Question

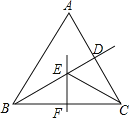
【题目】如图，在△ABC中，BC的垂直平分线EF交∠ABC的平分线BD于E，如果∠BAC＝60°，∠ACE＝24°，那么∠ABC的大小是（　　）

A.32°B.56°C.64°D.70°

Answer 1

【答案】C

【解析】

根据线段垂直平分线的性质得到EB＝EC，得到∠EBC＝∠ECB，根据角平分线的定义得到∠EBC＝∠EBA，根据三角形内角和定理列出算式，计算即可．

解：∵EF是BC的垂直平分线，

∴EB＝EC，

∴∠EBC＝∠ECB，

∵BD是∠ABC的平分线，

∴∠EBC＝∠EBA，

∴∠EBC＝∠ECB＝∠EBA，

由三角形内角和定理得，∠BAC+∠ACE+∠EBC+∠ECB+∠EBA=180°，

解得，∠EBC＝∠ECB＝∠EBA＝32°，

∴∠ABC＝64°，

故选：C．