Question

【题目】如图，半径为4的⊙O中，CD为直径，弦AB⊥CD且过半径OD的中点，点E为⊙O上一动点，CF⊥AE于点F．当点E从点B出发顺时针运动到点D时，点F所经过的路径长为（　　）

A. B. C. D.

Answer 1

【答案】C

【解析】

连接AC，AO，由AB⊥CD，利用垂径定理得到G为AB的中点，由中点的定义确定出OG的长，在直角三角形AOG中，由AO与OG的长，利用勾股定理求出AG的长，进而确定出AB的长，由CO+GO求出CG的长，在直角三角形AGC中，利用勾股定理求出AC的长，由CF垂直于AE，得到三角形ACF始终为直角三角形，点F的运动轨迹为以AC为直径的半径，如图中红线所示，当E位于点B时，CG⊥AE，此时F与G重合；当E位于D时，CA⊥AE，此时F与A重合，可得出当点E从点B出发顺时针运动到点D时，点F所经过的路径长，在直角三角形ACG中，利用锐角三角函数定义求出∠ACG的度数，进而确定出所对圆心角的度数，再由AC的长求出半径，利用弧长公式即可求出的长，即可求出点F所经过的路径长．

解：

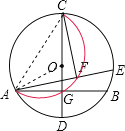
连接AC，AO，

∵AB⊥CD，

∴G为AB的中点，即AG=BG=AB，

∵⊙O的半径为4，弦AB⊥CD且过半径OD的中点，

∴OG=2，

∴在Rt△AOG中，根据勾股定理得：AG==2，

∴AB=2AG=4，

又∵CG=CO+GO=4+2=6，

∴在Rt△AGC中，根据勾股定理得：AC==4，

∵CF⊥AE，

∴△ACF始终是直角三角形，点F的运动轨迹为以AC为直径的半圆，

当E位于点B时，CG⊥AE，此时F与G重合；当E位于D时，CA⊥AE，此时F与A重合，

∴当点E从点B出发顺时针运动到点D时，点F所经过的路径长，

在Rt△ACG中，tan∠ACG==，

∴∠ACG=30°，

∴所对圆心角的度数为60°，

∵直径AC=4，

∴的长为=π，

则当点E从点B出发顺时针运动到点D时，点F所经过的路径长为π．

故选：C．