ЬтФПФкШн
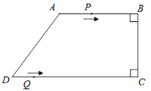
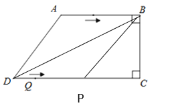
ЁОЬтФПЁПШчЭМЃЌдкЫФБпаЮABCDжаЃЌABЁЮCDЃЌЁЯABC=ЁЯBCD=90ЁуЃЌAD=10cmЃЌBC=8cmЃЌCD=16cmЃЎЕуPДгЕуAГіЗЂЃЌвдУПУы3cmЕФЫйЖШбиелЯпЖЮABЁЊBCЁЊCDдЫЖЏЃЌЕуQДгЕуDГіЗЂЃЌвдУПУы2cmЕФЫйЖШбиЯпЖЮDCЗНЯђЯђЕуCдЫЖЏЃЎвбжЊЖЏЕуPЁЂQЭЌЪБЗЂЃЌЩшдЫЖЏЪБМфЮЊtУыЃЈ![]() ЃЉЃЎ
ЃЉЃЎ
ЃЈ1ЃЉЧѓABЕФГЄЃЛ
ЃЈ2ЃЉЕБЫФБпаЮPBQDЮЊЦНааЫФБпаЮЪБЃЌЧѓЫФБпаЮPBQDЕФжмГЄЃЛ
ЃЈ3ЃЉдкЕуPдЫЖЏЙ§ГЬжаЃЌЕБ![]() УыЕФЪБКђЃЌЪЙЕУЁїBPDЕФУцЛ§ЮЊ20cm2ЃЎ
УыЕФЪБКђЃЌЪЙЕУЁїBPDЕФУцЛ§ЮЊ20cm2ЃЎ
ЁОД№АИЁПЃЈ1ЃЉ10ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]() Лђ
Лђ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉШчЭМ1жаЃЌзїAHЁЭCDгкHЃЎдђЫФБпаЮABCHЪЧОиаЮНтжБНЧШ§НЧаЮЧѓГіDHМДПЩНтОіЮЪЬтЃЛ
ЃЈ2ЃЉЕБЫФБпаЮPBQDЮЊЦНааЫФБпаЮЪБЃЌЕуPдкABЩЯЃЌЕуQдкDCЩЯЃЌИљОнPB=DQЙЙНЈЗНГЬНтОіЮЪЬтМДПЩЃЛ
ЃЈ3ЃЉЗжШ§жжЧщаЮЃКЂйЕБЕуPдкЯпЖЮABЩЯЪБЃЎЂкЕБЕуPдкЯпЖЮBCЩЯЪБЃЎЂлЕБЕуPдкЯпЖЮCDЩЯЪБЃЌЗжБ№РћгУШ§НЧаЮШ§НЧаЮУцЛ§ЙЋЪНСаЗНГЬМЦЫуЧѓНтМДПЩЃЎ
НтЃКЃЈ1ЃЉШчЭМ1жаЃЌзїAHЁЭCDгкHЃЎ
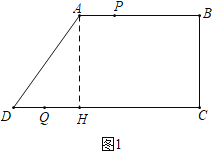
ЁпЁЯAHC=ЁЯB=ЁЯC=90ЁуЃЌ
ЁрЫФБпаЮABCHЪЧОиаЮЃЌ
ЁрAH=BC=8cmЃЌAB=CHЃЌ
дкRtЁїADHжаЃЌЁпЁЯAHD=90ЁуЃЌAD=10cmЃЌAH=8cmЃЌ
ЁрDH=![]() ЃЈcmЃЉЃЌ
ЃЈcmЃЉЃЌ
ЁрAB=CH=CD-DH=16-6=10ЃЈcmЃЉЃЎ
ЃЈ2ЃЉЕБЫФБпаЮ![]() ЮЊЦНааЫФБпаЮЪБЃЌ
ЮЊЦНааЫФБпаЮЪБЃЌ
![]() Чв
Чв![]() ЃЎ
ЃЎ
гЩЬтжЊЃКBP=10-3tЃЌDQ=2tЃЌ
Ёр![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]()
Ёр![]() ЃЌ
ЃЌ
Ёр![]()
Ёр![]()
![]()
ЁрЦНааЫФБпаЮ![]() ЕФжмГЄ
ЕФжмГЄ![]() ЃЎ
ЃЎ

ЃЈ3ЃЉЕБ![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯЪБЃЌ
ЩЯЪБЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌНтЕУ
ЃЌНтЕУ![]()
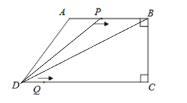
ЕБ![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯЪБЃЌ
ЩЯЪБЃЌ![]() ЃЌ
ЃЌ
![]() ЃЌНтЕУ
ЃЌНтЕУ![]()
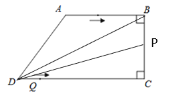
ЕБЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯЪБЃЌDP=34-3t
ЩЯЪБЃЌDP=34-3t
![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЈгЩ
ЃЈгЩ![]() ЃЌЫљвдДЫНтЩсШЅЃЉЃЌ
ЃЌЫљвдДЫНтЩсШЅЃЉЃЌ
злЩЯЫљЪіЃЌ![]() ЃЌЛђ
ЃЌЛђ![]() Уы
Уы

 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ



