题目内容
【题目】如图,二次函数![]() 的图象与x轴交于点A,B,与y轴交于点C.点P是该函数图象上的动点,且位于第一象限,设点P的横坐标为x.
的图象与x轴交于点A,B,与y轴交于点C.点P是该函数图象上的动点,且位于第一象限,设点P的横坐标为x.
(1)写出线段AC, BC的长度:AC= ,BC= ;
(2)记△BCP的面积为S,求S关于x的函数表达式;
(3)过点P作PH⊥BC,垂足为H,连结AH,AP,设AP与BC交于点K,探究:是否存在四边形ACPH为平行四边形?若存在,请求出![]() 的值;若不存在,请说明理由,并求出
的值;若不存在,请说明理由,并求出![]() 的最大值.
的最大值.
【答案】(1)AC=![]() ,BC=
,BC=![]() ;(2)y
;(2)y![]() ;(3)
;(3) ![]() .
.
【解析】试题分析:求出与坐标轴的交点坐标,然后根据勾股定理求解;
(2)利用割补法列式,即根据![]() 列式;
列式;
(3)过点P作PH⊥BC于H,根据一组对边及平行又相等的四边形是平行四边形判断;由△AKC∽△PHK列比例式求解.
解;(1)AC=![]() ,BC=
,BC=![]() ;
;
(2)设P(x, ![]() ),则有
),则有![]()
=![]() =
=![]()
(3)过点P作PH⊥BC于H,
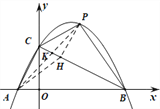
∵![]() ,
,
∴△ABC为直角三角形,即AC⊥BC;∴AC∥PH,
要使四边形ACPH为平行四边形,只需满足PH=AC=![]() ,
,
∴![]() =5,而
=5,而![]() =
=![]() =
=![]() ,
,
所以不存在四边形ACPH为平行四边形
由△AKC∽△PHK,
∴![]() =
=![]() (当x=2时,取到最大值)
(当x=2时,取到最大值)

练习册系列答案
相关题目
【题目】在生活与工作都离不开手机和电脑的今天,青少年近视、散光等眼问题日趋严重,为宣传2018全国爱眼日(6月6日),增强大众近视防控意识,某青少年视力矫正中心举办了主题为“永康降度还您一双明亮的眼睛”的降度明星大赛,现根据大赛公布的结果,将所有参赛孩子双眼降度之和(含近视和散光)情况绘制成了如下的统计表:
所降度数(度) | 100 | 200 | 300 | 400 | 500 | 600 |
人数(人) | 12 | 18 | 24 | 4 | 1 | 1 |
(1)求参加降度明星大赛的孩子共有多少人?
(2)求出所有参赛孩子所降度数的众数、中位数和平均数.