题目内容
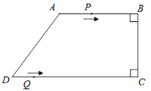
【题目】如图，等腰三角形纸片ABC中，AD⊥BC与点D，BC=2，AD=
，沿AD剪成两个三角形．用这两个三角形拼成平行四边形，该平行四边形中较长对角线的长为__________．
【答案】2或
或
【解析】
分别以AC，AD， BD为对角线拼成平行四边形，然后利用勾股定理求解
解：由题意可知，等腰△ABC中，AD⊥BC
∴BD=CD=
，AC=
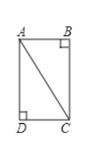
①当以AC边为对角线时，此时平行四边形ADCB为矩形，两对角线长度相等为2；
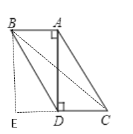
②当以AD边为对角线时，此时平行四边形BDCA的较长对角线是BC，
过点B作BE⊥CD，交CD的延长线于点E
此时四边形BEDA为矩形
∴BE=AD=
，DE=AB=1，EC=DE+CD=2
∴在Rt△BEC中，
③当以BD为对角线时，此时平行四边形ADCB的较长对角线是AC
过点C作CE⊥AD，交AD的延长线于点E
此时四边形DECB是矩形
∴DE=BC=AD=，CE=BD=1，AE=AD+DE=
∴在Rt△AEC中，AC=
综上，平行四边形中较长对角线的长为2或或
故答案为：2或或．
培优三好生系列答案
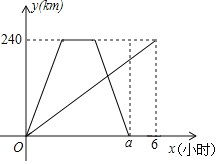
优化作业上海科技文献出版社系列答案【题目】某校七年级开展了为期一周的“敬老爱亲”社会活动，并根据学生做家务的时间来评价他们在活动中的表现，学校随机抽查了部分学生在这次活动中做家务的时间，并绘制了如下的频数分布表和频数分布直方图．请根据图表中提供的信息，解答下列问题：
等级 | 做家务时间（小时） | 频数 | 百分比 |
A | 0.5≤x＜1 | 3 | 6% |
B | 1＜x＜1.5 | a | 30% |
C | 1.5≤x＜2 | 20 | 40% |
D | 2≤x＜2.5 | b | m |
E | 2.5≤x＜3 | 2 | 4% |
（1）这次活动中抽查的学生有______人，表中a=______，b=______，m=______，并补全频数分布直方图；
（2）若该校七年级有700名学生，请估计这所学校七年级学生一周做家务时间不足2小时而又不低于1小时的大约有多少人？
