Question

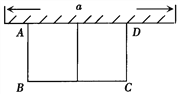
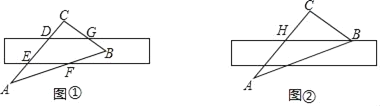
【题目】将直尺摆放在三角板上，使直尺与三角板的边分别交于点D、E、F、G，如图①所示．已知∠CGD＝42．

（1）求∠CEF的度数．

（2）将直尺向下平移，使直尺的边缘通过点B，交AC于点H，如图②所示．点H、B的读数分别为4、13.4，求BC的长（精确到0.1）（参考数据：sin42°＝0.67，cos42°＝0.74，tan42°＝0.90）

Answer 1

【答案】（1）48°；（2）BC的长为7.0

【解析】

（1）先根据直角三角形的两锐角互为求出∠CDG的度数，再根据两直线平行，同位角相等求出∠CEF；

（2）根据读数求出HB的长度，再根据∠CBH＝∠CGD＝42°，利用42°的余弦值求解．

（1）∵∠CGD＝42°，∠C＝90°，

∴∠CDG＝90°﹣42°＝48°，

∵DG∥EF,

∴∠CEF＝∠CDG＝48°；

（2）∵点H、B的读数分别为4、13.4，

∴HB＝13.4﹣4＝9.4，

∴BC＝HBcos42°＝9.4×0.74≈7.0，

答：BC的长为7.0