Question

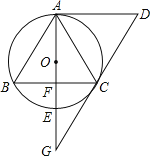
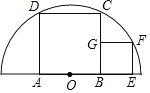
【题目】正方形ABCD、正方形BEFG，点A、B、E在半圆O的直径上，点D、C、F在半圆O上，若EF＝4，则该半圆的半径为（　　）

A.B.8C.D.

Answer 1

【答案】A

【解析】

先根据正方形的性质得CB＝AB，AB=2OB＝2OA，设OB＝x，则OE＝x+4，BC＝2x，再根据勾股定理，在Rt△COB中有OC2＝OB2+CB2＝5x2，在Rt△OEF中有OF2＝OE2+EF2＝（x+4）2+42，则（x+4）2+42＝5x2，然后解方程得到x＝4，再利用CO＝x进行计算即可．

解：如图，连接OD、OC、OF，

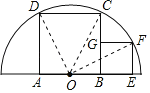
∵四边形ABCD为正方形，

∴CB＝AB，AB=2OB＝2OA，

设OB＝x，则OE＝x+4，CB＝2x，

在Rt△CBO中，OC2＝OB2+CB2＝x2+（2x）2＝5x2，

在Rt△OEF中有OF2＝OE2+EF2＝（x+4）2+42，

而OC＝OF，

∴（x+4）2+42＝5x2，

整理得x2﹣2x﹣8＝0，

解得x1＝4，x2＝﹣2（舍去），

∴OC＝x＝4，

即该圆的半径为4．

故选：A．