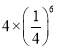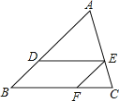Question

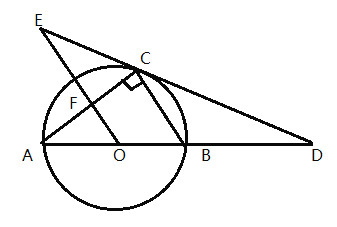
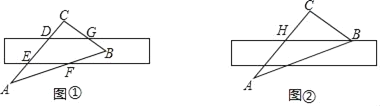
【题目】如图1，△ABC中，∠B＝30°，点D在BA的延长线上，点E在BC边上，连接DE，交AC于点F．若∠EFC＝60°，DE＝2AC，求的值．某学习小组的同学经过思考，交流了自己的想法：

小明：“通过观察和度量，发现∠C与∠D存在某种数量关系”；

小强：“通过构造三角形，证明三角形相似，进而可以求得的值．

老师：如图2，将原题中“点D在BA的延长线上，点E在BC边上”改为“点D在AB边上，点E在BC的延长线上”，添加条件“BC＝5，EC＝4”，其它条件不变，可求出△BED的面积．

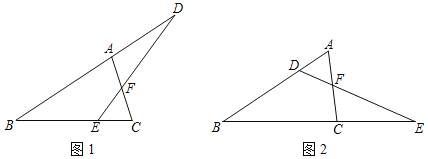
请回答：

（1）用等式表示∠C、∠D的数量关系并证明；

（2）求的值；

（3）△BDE的面积为　 　（直接写出答案）．

Answer 1

【答案】（1）∠C+∠D＝90°，见解析；（2）；（3）18

【解析】

（1）结论：∠C+∠D＝90°．利用三角形的内角和定理解决问题即可．

（2）过点A作AG⊥BC垂足为G，交DE点Q，过点E作EH⊥BD垂足为H，则∠DHE＝∠BHE＝90°．利用相似三角形的性质解决问题即可．

（3）如图2中，在BA上取一点G，使得GB＝GC，作GJ⊥BC于J，AH⊥CG于H，EK⊥BA交BA的延长线于K．利用相似三角形的性质解决问题即可．

解：（1）结论：∠C+∠D＝90°．

理由：如图1中，

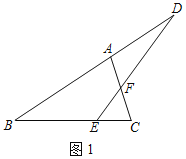
∵∠AFD=∠EFC=60°，

∵∠BAC＝180°﹣∠C﹣30°＝150°﹣∠C，∠BAC＝∠AFD+∠D＝60°+∠D，

∴150°﹣∠C＝60°+∠D，

∴∠C+∠D＝90°．

（2）过点A作AG⊥BC垂足为G，交DE点Q，过点E作EH⊥BD垂足为H，则∠DHE＝∠BHE＝90°．

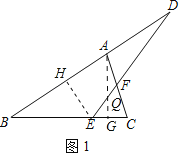
∵∠AGC＝90°，

∴∠DHE═∠AGC．

∵∠C+∠D＝90°, ∠C+∠CAG＝90°．

∴∠D＝∠CAG，

∴△DEH∽△ACG．

∴．

∴DH＝2AG．

∵∠B＝30°，∠AGB＝90°，

∴AB＝2AG．

∴AB＝DH．

∴AB﹣AH＝DH﹣AH．

即BH＝AD．

在Rt△BHE中，＝cos30°＝．

∴＝＝．

（3）如图2中，在BA上取一点G，使得GB＝GC，作GJ⊥BC于J，AH⊥CG于H，EK⊥BA交BA的延长线于K．

∵∠BAC＝180°﹣∠B﹣∠ACB＝180°﹣∠ADE﹣∠AFD，

∴150°﹣∠ACB＝120°﹣∠ADF，

∴∠ACB﹣30°＝∠ADE，

∵GB＝GC，GJ⊥BC，

∴∠GCB＝∠B＝30°，BJ＝JC=＝，

∴∠ACH＝∠ACB﹣30°＝∠EDK，BG＝CG＝＝5，

∵∠ACH＝∠EDK，∠AHC＝∠K＝90°，

∴△DEK∽△CAH，

∴，

在Rt△BKE中，∵∠K＝90°，∠B＝30°，BE＝9，

∴EK＝，BK＝，

∴AH＝，

∴GH＝AH＝，

∴CH＝CG﹣GH＝，

∴DK＝2CH＝，

∴BD＝BK﹣DK＝﹣＝8，

∴S△BDE＝BD·EK＝×8×＝18．

故答案为18．