题目内容
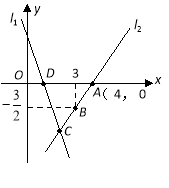
【题目】如图,在平面直角坐标系中,点A、B分别在x轴、y轴上,线段OA、OB的长(OA<OB)是一元二次方程x2﹣18x+72=0组的解.点C是直线y=2x与直线AB的交点,点D在线段OC上,OD=2![]() .
.
(1)求点C的坐标;
(2)求直线AD的解析式;
(3)P是直线AD上的点,在平面内是否存在点Q,使以O、A、P、Q为顶点的四边形是菱形?若存在,则求出点Q的坐标;若不存在,请说明理由.

【答案】(1)C的坐标为(3,6);(2)y=﹣x+6;(3)存在,Q的坐标为(﹣3![]() ,3
,3![]() )或(3
)或(3![]() ,﹣3
,﹣3![]() )或(3,﹣3)或(6,6).
)或(3,﹣3)或(6,6).
【解析】
(1)设直线AB的解析为y=kx+b,解方程x2﹣18x+72=0,得到的解即为OA,OB的长度,进而知道A和B的坐标,再把其横纵坐标分别代入求出k和b的值即可;把求出的解析式和直线y=2x联立解方程组,方程组的解即为点C的坐标.
(2)要求直线AD的解析式,需求出D的坐标,因为点D在直线OC上因此可设D(a,2a),又因为OD=2![]() ,由勾股定理可求出a的值,从而求得点D的坐标,把A、D的坐标代入,利用方程组即可求解.
,由勾股定理可求出a的值,从而求得点D的坐标,把A、D的坐标代入,利用方程组即可求解.
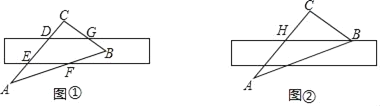
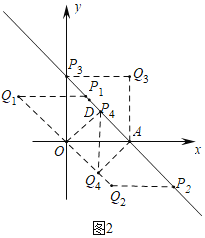
(3)分四种情形:如图2中,当四边形OAP1Q1是菱形时.当四边形OAP2Q2是菱形时.当四边形AOQ3P3是菱形时.当四边形OP4AQ4是菱形时,分别求解即可解决问题.
(1)解方程x2﹣18x+72=0,得到x=6或12,
∵线段OA、OB的长(0A<OB)是方程组的解,
∴OA=6,OB=12,
∴A(6,O),B(0,12),
设直线AB的解析为y=kx+b,
∴![]() ,
,
∴直线AB:y=﹣2x+12,
联立![]() ,
,
解得:![]() ,
,
点C的坐标为(3,6)
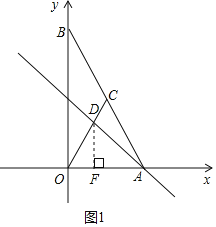
(2)如图1中,设点D:(a,2a),作DF⊥OA于F.
由OD=2![]() ,OF=a,DF=2a,可得a2+(2a)2=(2
,OF=a,DF=2a,可得a2+(2a)2=(2![]() )2,
)2,
得:a=±2,
∵由图得,a>0,
∴a=2.
∴D(2,4),
设直线AD的解析式为y=kx+b
把A(6,0),D(2,4)代入得![]() ,
,
解得![]() ,
,
∴直线AD的解析式为y=﹣x+6;
(3)存在.如图2中,
当四边形OAP1Q1是菱形时,AO=AP1=P1Q1=6,
∵∠DAO=45°,
∴P1(6﹣3![]() ,3
,3![]() ),
),
∴Q1(﹣3![]() ,3
,3![]() ),
),
当四边形OAP2Q2是菱形时,同法可得Q2(3![]() ,﹣3
,﹣3![]() ),
),
当四边形AOQ3P3是菱形时,∵∠AOP3=90°,
∴四边形OAQ3P3是正方形,可得Q3(6,6),
当四边形OP4AQ4是菱形时,
∵∠DAO=∠OAQ4=45°
∴∠P4AQ4=90°,
∴四边形OP4AQ4是正方形,
∴Q4(3,﹣3),
综上所述,满足条件的点Q的坐标为(﹣3![]() ,3
,3![]() )或(3
)或(3![]() ,﹣3
,﹣3![]() )或(3,﹣3)或(6,6).
)或(3,﹣3)或(6,6).

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案