题目内容
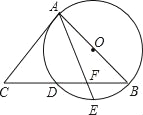
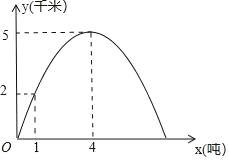
【题目】如图①，在A、B两地之间有汽车站C，客车由A地驶往C站，货车由B地驶往A地，两车同时出发，匀速行驶，图②是客车、货车离 C站的路程
、
(km)与行驶时间x(h)之间的函数图像．
(1)客车的速度是 km/h；
(2)求货车由 B地行驶至 A地所用的时间；
(3)求点E的坐标，并解释点 E的实际意义．
【答案】（1）60；（2）14h；（3）点E代表的实际意义是在行驶
h时，客车和货车相遇，相遇时两车离C站的距离为80km．
【解析】
（1）由图象可知客车6小时行驶的路程是360km，从而可以求得客车的速度；
（2）由图象可以得到货车行驶的总的路程，前2h行驶的路程是60km，从而可以起求得货车由B地行驶至A地所用的时间；
（3）根据图象利用待定系数法分别求得EF和DP所在直线的解析式，然后联立方程组即可求得点E的坐标，根据题意可以得到点E代表的实际意义．
解：（1）由图象可得，客车的速度是：360÷6=60（km/h），
故答案为：60；
（2）由图象可得，
货车由B地到A地的所用的时间是：（60+360）÷（60÷2）=14（h），
即货车由B地到A地的所用的时间是14h；
（3）设客车由A到C对应的函数解析式为y=kx+b，
则
，得
，
即客车由A到C对应的函数解析式为y=-60x+360；
根据（2）知点P的坐标为（14，360），设货车由C到A对应的函数解析式为y=mx+n，
则
，得
，
即货车由C到A对应的函数解析式为y=30x-60；
∴
，得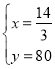
，
∴点E的坐标为（，80），
故点E代表的实际意义是在行驶h时，客车和货车相遇，相遇时两车离C站的距离为80km．
【题目】我区浙江中国花木城组织10辆汽车装运完A、B、C三种不同品质的苗木共100吨到外地销售，按计划10辆汽车都要装满，且每辆汽车只能装同一种苗木，由信息解答以下问题：
苗 木 品 种 | A | B | C |
每辆汽车运载量（吨） | 12 | 10 | 8 |
每吨苗木获利（万元） | 3 | 4 | 2 |
（1）设装A种苗木车辆数为x，装运B种苗木的车辆数为y，求y与x之间的函数关系式；
（2）若装运每种苗木的车辆都不少于2辆，则车辆安排方案有几种？写出每种安排方案
（3）若要使此次销售获利最大，应采用哪种安排方案？并求出最大利润．
