题目内容
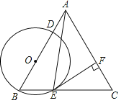
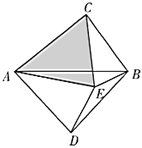
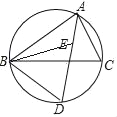
【题目】如图，点E是△ABC的内心，AE的延长线与△ABC的外接圆相交于点D．
(1)若∠BAC=70°，求∠CBD的度数；
(2)求证：DE=DB．
【答案】（1）35°；（2）证明见解析.
【解析】
（1）由点E是△ABC的内心，∠BAC=70°，易得∠CAD=
，进而得出∠CBD=∠CAD=35°；
(2) 由点E是△ABC的内心，可得E点为△ABC角平分线的交点，可得∠ABE=∠CBE，∠BAD=∠CAD，可推导出∠DBE=∠BED，可得DE=DB.
（1）∵点E是△ABC的内心，∠BAC=70°，
∴∠CAD=
，
∵
，
∴∠CBD=∠CAD=35°；
（2）∵E是内心，
∴∠ABE=∠CBE，∠BAD=∠CAD．
∵∠CBD=∠CAD，
∴∠CBD=∠BAD，
∵∠BAD+∠ABE=∠BED，∠CBE+∠CBD=∠DBE，
∴∠DBE=∠BED，
∴DE=DB.
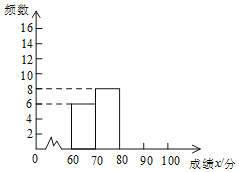
名校课堂系列答案
【题目】中华文明，源远流长，中华汉字，寓意深广，为了传承优秀传统文化，某校九年级组织600名学生参加了一次“汉字听写”大赛
赛后发现所有参赛学生的成绩均不低于60分，为了更好地了解本次大赛的成绩分布情况，随机抽取了其中若干名学生的成绩作为样本，成绩如下：
90，92，81，82，78，95，86，88，72，66，62，68，89，86，93，97，100，73，76，80，77，81，86，89，82，85，71，68，74，98，90，97，100，84，87，73，65，92，96，60．
对上述成绩进行了整理，得到下列不完整的统计图表：
成绩 | 频数 | 频率 |
| 6 |
|
| 8 |
|
| a | b |
| c | d |
请根据所给信息，解答下列问题：
______，
______，
______，
______；
请补全频数分布直方图；
若成绩在90分以上
包括90分
的为“优”等，请你估计参加这次比赛的600名学生中成绩“优”等的约有多少人？
