题目内容
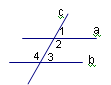
.如图,在等腰梯形ABCD中,AD∥BC,对角线AC⊥BD于点O,AE⊥BC,DF⊥BC,垂足分别为E、F,AD=4,BC=8,则AE+EF= 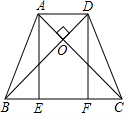

10
过D点作AC的平行线,交BC的延长线于G点,
∵AD∥BC,
∴四边形ADGC为平行四边形,
∴DG=AC,
∵AC⊥BD,
∴DG⊥BD,
∵等腰梯形ABCD,
∴AC=BD,
∴DG=BD,
∴△DBG为等腰直角三角形,
∴∠G=∠ACE=45°,
∴AE=CE=6,
∴FC=6-4=2,
∴EF=BC-2FC=8-2FC=4,
∴AE+EF=6+4=10.
故选B.
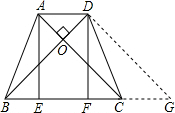
∵AD∥BC,
∴四边形ADGC为平行四边形,
∴DG=AC,
∵AC⊥BD,
∴DG⊥BD,
∵等腰梯形ABCD,
∴AC=BD,
∴DG=BD,
∴△DBG为等腰直角三角形,
∴∠G=∠ACE=45°,
∴AE=CE=6,
∴FC=6-4=2,
∴EF=BC-2FC=8-2FC=4,
∴AE+EF=6+4=10.
故选B.


练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目

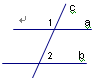
 ,∠1=45°,则∠2=_____.
,∠1=45°,则∠2=_____. 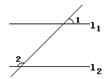
 在
在 上,且
上,且 ,点
,点 是
是 延长线上一点,
延长线上一点, ,联结
,联结 与
与 交于点
交于点 ,求
,求 的值.
的值.