��Ŀ����
����Ŀ�������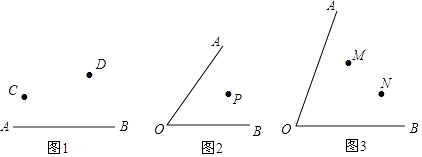
��1����ͼ1����ABֱ��һ��C��D���㣬��AB����һ��P��ʹC��D��P������ɵ������ε��ܳ���̣��ҳ��˵㲢˵�����ɣ�
��2����ͼ2���ڡ�AOB�ڲ���һ��P���Ƿ���OA��OB�Ϸֱ���ڵ�E��F��ʹ��E��F��P������ɵ������ε��ܳ���̣��ҳ�E��F���㣬��˵�����ɣ�
��3����ͼ3���ڡ�AOB�ڲ�������M��N���Ƿ���OA��OB�Ϸֱ���ڵ�E��F��ʹ��E��F��M��N���ĵ���ɵ��ı��ε��ܳ���̣��ҳ�E��F���㣬��˵�����ɣ�
���𰸡�
��1��
�⣺��ͼ1����C����ֱ��AB�ĶԳƵ�C�䣬
����C��D��AB�ڵ�P��
���P������Ҫ�����ĵ㣮
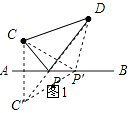
���ɣ���l��ȡ��ͬ��P�ĵ�P�䣬����CP�䡢DP�䣮
��C��C�����ֱ��l�Գƣ�
��PC=PC�䣬P��C=P��C�䣬
��C��P+DP��C��P��+DP�䣬
��PC+DP��CP��+DP��
��CD+CP+DP��CD+CP��+DP��
����CDP�ܳ�С�ڡ�CDP���ܳ�
��2��
�⣺��ͼ2����P����OA�ĶԳƵ�C������OB�ĶԳƵ�D������CD����OA��E��OB��F��
���E��F������Ҫ�����ĵ㣮

���ɣ���OA��OB��ȡ��ͬ��E��F�ĵ�E�䣬F�䣬����CE�䡢E��P�䣬
��C��P����ֱ��OA�Գƣ�
��PE=CE��CE��=PE�䣬PF=DF��PF��=DF�䣬
��PE+EF+PF=CE+EF+DF��PE��+PF��+E��F��=CE��+E��F��+DE�䣬
��CE+EF+DF��CE��+E��F��+DF�䣬��
��PE+EF+PF��PE��+PF��+E��F��
��3��
�⣺��ͼ3����M����OA�ĶԳƵ�C������OB�ĶԳƵ�D������CD����OA��E��OB��F��
���E��F������Ҫ�����ĵ㣮

���ɣ���OA��OB��ȡ��ͬ��E��F�ĵ�E�䣬F�䣬����CE�䡢E��P�䣬
��C��P����ֱ��OA�Գƣ�
��PE=CE��CE��=PE�䣬PF=DF��PF��=DF�䣬
�ɣ�2����֪MN+ME+EF+MF��ME��+E��F��+F��D��
����������1�����ڡ�PCD���ܳ�=PC+CD+PD����CD�Ƕ�ֵ����ֻ����ֱ��l����һ��P��ʹPC+PD��С�������C����l�ĶԳƵ�ΪC�䣬ʹPC+PD��С����ʹPC��+PD��С����2����P����OA��OB�ĶԳƵ�C��D������CD��OA��OB��E��F����ʱ��PEF�ܳ�����Сֵ����3����ͼ3����M����OA�ĶԳƵ�C������OB�ĶԳƵ�D������CD����OA��E��OB��F����ʱʹ��E��F��M��N���ĵ���ɵ��ı��ε��ܳ���̣�
�����㾫�����������⣬������Ҫ�˽���ԳƵ�����(����ij��ֱ�߶ԳƵ�����ͼ����ȫ���Σ��������ͼ�ι���ijֱ�߶Գƣ���ô�Գ����Ƕ�Ӧ�����ߵĴ�ֱƽ���ߣ�����ͼ�ι���ijֱ�߶Գƣ�������ǵĶ�Ӧ�߶λ��ӳ����ཻ����ô�����ڶԳ�����)����Ҫ������Գ�-���·������(��֪����㣬�����·������ȷ������෴����֪�յ��㣬�����·������֪�����յ㣬�������֮������·������ͼ���������·��)�����֪ʶ���Ǵ���Ĺؼ���

 ��У����ϵ�д�
��У����ϵ�д�