��Ŀ����
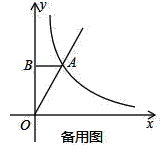
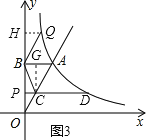
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y=kx��˫����![]() �ڵ�һ�����ཻ�ڵ�A��1��2������B��y���ϣ���AB��y�ᣮ��һ����P��ԭ�������y����ÿ��1����λ���ٶ���y����������˶����˶�ʱ��Ϊt�루t��0��������P��PD��y�ᣬ��ֱ��OA�ڵ�C����˫�����ڵ�D��
�ڵ�һ�����ཻ�ڵ�A��1��2������B��y���ϣ���AB��y�ᣮ��һ����P��ԭ�������y����ÿ��1����λ���ٶ���y����������˶����˶�ʱ��Ϊt�루t��0��������P��PD��y�ᣬ��ֱ��OA�ڵ�C����˫�����ڵ�D��
��1����ֱ��y=kx��˫����![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��2�����ı���CDAB�����ΪS����P���߶�OB���˶�ʱ��P����B���غϣ�����S��t֮��ĺ�����ϵʽ��
��3����ͼ�е�һ����˫�������Ƿ���ڵ�Q��ʹ��A��B��C��Q�ĵ�Ϊ������ı�����ƽ���ı��Σ������ڣ��������ʱt��ֵ��Q������ꣻ�������ڣ���˵�����ɣ�

���𰸡���1��![]() ��
��![]() ����2��
����2��![]() ����3��
����3��![]() ʱ��Q
ʱ��Q![]() ��
��![]() ʱ��Q
ʱ��Q![]() ��
��![]() ʱ��
ʱ��![]() ��
��
��������
��1���ѵ�A������������������Ľ���ʽ���k��k����ֵ���ɵõ����������Ľ���ʽ��
��2����������AB=1��OB=2��OP=t����ϣ�1�����������������Ľ���ʽ�ɵã�PC=![]() ��PD=
��PD=![]() ��BP=
��BP=![]() ���ɴ˿ɵõ���P���߶�AB�ϣ������B�غϣ�ʱ��CD=PD-PC=
���ɴ˿ɵõ���P���߶�AB�ϣ������B�غϣ�ʱ��CD=PD-PC=![]() ������S=S����ABCD=
������S=S����ABCD=![]() ��AB+CD����BP�������S��t��ĺ�����ϵʽ�ˣ�
��AB+CD����BP�������S��t��ĺ�����ϵʽ�ˣ�
��3���������⣬����CD��AB���·���AB��CD����AB=CD����Q���D�غϣ���CD��AB�Ϸ���AB��CD����AB=CD����Q���D�غϣ���CD��AB�·���BQ��AC��BQ=AC���������������������Ӧ��ͼ�Σ�ͼ2��ͼ3�������֪�������з������.
��1����A��1��2������y=kx��y=![]() ��
��
k=2��k��=2
��ֱ��y=kx�ĺ�����ϵʽ��y=2x��˫����y=![]() �ĺ�����ϵʽ��y=
�ĺ�����ϵʽ��y=![]() ��
��
��2��������ɵ���AB=1��OB=2��OP=t��
��PC=![]() ��PD=
��PD=![]() ��BP=2-t��
��BP=2-t��
�൱CD��AB�·�ʱ��CD=PD-PC=![]() -
-![]() ��
��
��S=![]() (1+
(1+![]() -
-![]() )(2-t)=
)(2-t)= ![]() ��0��t��2����
��0��t��2����
��3����������3�����Σ��������£�
����CD��AB���·���AB��CD����AB=CD����Q���D�غ�����ͼ2��ʱ���ı���ABCQ��ƽ���ı�����
��CD=PD-PC=![]() -
-![]() =1��
=1��
��![]() �����
�����![]() ����ȥ����
����ȥ����
����ʱPD=![]() =
=![]() ��OP=t=
��OP=t=![]() -1��
-1��
�൱t=![]() -1ʱ������Q��
-1ʱ������Q��![]() ��
��![]() -1��ʹ��A��B��C��Q�ĵ�Ϊ������ı�����ƽ���ı��Σ�
-1��ʹ��A��B��C��Q�ĵ�Ϊ������ı�����ƽ���ı��Σ�
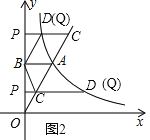
����CD��AB���Ϸ���AB��CD����AB=CD����Q���D�غ�����ͼ2��ʱ���ı���ACBQ��ƽ���ı��Σ�
��CD=PC-PD��
��![]() ����ã�
����ã�![]() ����ȥ����
����ȥ����
����ʱPD=![]() =
=![]() ��OP=t=
��OP=t=![]() +1��
+1��
�൱t=![]() +1ʱ������Q��
+1ʱ������Q��![]() ��
��![]() +1��ʹ��A��B��C��Q�ĵ�Ϊ������ı�����ƽ���ı��Σ�
+1��ʹ��A��B��C��Q�ĵ�Ϊ������ı�����ƽ���ı��Σ�
����BQ��AC��BQ=AC����CD��AB�·�ʱ����ͼ3������ʱ�ı���ACBQ��ƽ���ı��Σ�
��ʱQ���������Ϊ��![]() ��
��![]() +1����
+1����
��C��CG��AB��AB��G����Q��QH��y�ύy����H��
��֤����ACG�ա�QBH��
��CG=BH=BP����
��OP=2OB-OH=4-��![]() +1��=3-
+1��=3-![]() ��
��
�൱t=3-![]() ʱ������Q��
ʱ������Q��![]() ��
��![]() +1��ʹ��A��B��C��Q�ĵ�Ϊ������ı�����ƽ���ı��Σ�
+1��ʹ��A��B��C��Q�ĵ�Ϊ������ı�����ƽ���ı��Σ�

 ��ʱѵ���������������ϵ�д�
��ʱѵ���������������ϵ�д� �ƸԾ���Ȥζ����ϵ�д�
�ƸԾ���Ȥζ����ϵ�д�