题目内容
【题目】如图,点A是反比例函数y=﹣ ![]() 在第二象限内图象上一点,点B是反比例函数y=
在第二象限内图象上一点,点B是反比例函数y= ![]() 在第一象限内图象上一点,直线AB与y轴交于点C,且AC=BC,连接OA、OB,求△AOB的面积.
在第一象限内图象上一点,直线AB与y轴交于点C,且AC=BC,连接OA、OB,求△AOB的面积.
【答案】解:分别过A、B两点作AD⊥x轴,BE⊥x轴,垂足为D、E,
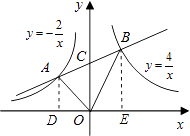
∵AC=CB,∴OD=OE,
设A(﹣a, ![]() ),则B(a,
),则B(a, ![]() ),
),
故S△AOB=S梯形ADBE﹣S△AOD﹣S△BOE
= ![]() (
( ![]() +
+ ![]() )×2a﹣
)×2a﹣ ![]() a×
a× ![]() ﹣
﹣ ![]() a×
a× ![]() =3.
=3.
【解析】分别过A、B两点作AD⊥x轴,BE⊥x轴,垂足为D、E,可证明AD∥OC∥BE,由AC=CB,根据平行线等分线段,得出OD=OE,设出点A、B的坐标,由S△AOB=S梯形ADBE﹣S△AOD﹣S△BOE即可求出结果。
【考点精析】通过灵活运用直角梯形和平行线分线段成比例,掌握一腰垂直于底的梯形是直角梯形;三条平行线截两条直线,所得的对应线段成比例即可以解答此题.

练习册系列答案
相关题目