题目内容
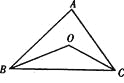
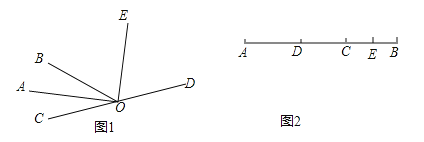
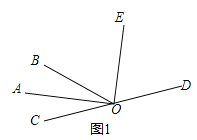
【题目】(1)如图1,已知O是直线CD上的点,OA平分∠BOC,OE平分∠BOD,∠AOC=35°,求∠BOE,∠COE的度数.
(2)如图2,已知AB=16cm,C是AB上一点,点D是线段AC的中点,点E是线段BC的中点,求线段DE的长度.
【答案】(1)125°;(2)8cm.
【解析】试题分析:(1)已知OA平分∠BOC,∠AOC=70°,根据角平分线的定义可得∠BOD=110°,再由OE平分∠BOD,可得∠BOE=55°,根据∠COE=∠BOC+∠BOE即可求得∠COE的度数;(2)已知点D是线段AC的中点,点E是线段BC的中点,根据线段中点的定义可得DC=![]() AC,CE=
AC,CE=![]() CB,根据DE=DC+CE=
CB,根据DE=DC+CE=![]() (AC+CB)即可求得DE的长度.
(AC+CB)即可求得DE的长度.
试题解析:
(1)∵OA平分∠BOC,
∴∠BOC=2∠AOC=70°,
∴∠BOD=110°,
∵OE平分∠BOD,
∴∠BOE=55°,
∴∠COE=∠BOC+∠BOE=125°;
(2)∵点D是线段AC的中点,点E是线段BC的中点,
∴DC=![]() AC,CE=
AC,CE=![]() CB,
CB,
∴DE=DC+CE=![]() (AC+CB)=8cm.
(AC+CB)=8cm.
![]()

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
相关题目