��Ŀ����
����Ŀ��ij���ڵ�·��������У���Ҫ����һ����Ϊ1000�Ĺܵ��������ɼס����������̶��������һ���̣���֪���̶ӱ��ҹ��̶�ÿ���ܶ�����20�ף��Ҽ��̶�����350�����õ��������ҹ��̶�����250�����õ�������ͬ��
��1���ס��ҹ��̶�ÿ�������������ף�
��2�����Ҫ����ɸ���̵Ĺ��ڲ�����10�죬��ôΪ�����̶ӷ��乤�����ķ����м��֣����������Ƴ��������̶ӷ��乤����Ϊ������������
���𰸡�
��1���⣺����̶�ÿ��������x�ף����ҹ��̶�ÿ�������裨x��20���ף�
��������ã� ![]() ��
��
��350��x��20��=250x��
��7x��140=5x
���x=70��
�����飬x=70��ԭ��ʽ���̵Ľ⣬�ҷ������⣬
�ҹ��̶�ÿ�������裺x��20=70��20=50�ף�
�𣺼ס��ҹ��̶�ÿ��ֱ�������70��50��
��2���⣺���������̶�y�ף��������ҹ��̶ӣ�1000��y���ף�
�����⣬��
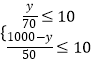 ��
��
���500��y��700��
���Է��䷽����3�֣�
����һ����������̶�500�ף�������ҹ��̶�500�ף�
����������������̶�600�ף�������ҹ��̶�400�ף�
����������������̶�700�ף�������ҹ��̶�300��
����������1������̶�ÿ��������x�ף����ݼ��̶�����350�����õ��������ҹ��̶�����250�����õ�������ͬ���з�����⣻��2�����������̶�y�ף��������ҹ��̶ӣ�1000��y���ף�������ɸ���̵Ĺ��ڲ�����10�죬�в���ʽ����з�����
�����㾫����������Ҫ�����˷�ʽ���̵�Ӧ�ú�һԪһ�β���ʽ���Ӧ�õ����֪ʶ�㣬��Ҫ�����з�ʽ���̽�Ӧ����IJ��裺���⡢��δ֪��������ȹ�ϵ�з��̡��ⷽ�̲������д���𰸣�Ҫ�е�λ����1���������⣬�ҳ����ȹ�ϵ��2���裺��δ֪����3���У��г�����ʽ�飻4���⣺�ⲻ��ʽ�飻5�����飺�Ӳ���ʽ��Ľ⼯���ҳ���������Ĵ𰸣�6����д������𰸲�����ȷ�����⣮

 ��1����Ԫ�¿�������ĩϵ�д�
��1����Ԫ�¿�������ĩϵ�д�����Ŀ��ij��ȥˮ�������г��ɹ�ƻ������������![]() ��
�� ![]() ����ƻ����������ƻ��Ʒ��һ�������ۼ۶�Ϊ
����ƻ����������ƻ��Ʒ��һ�������ۼ۶�Ϊ![]() Ԫ/ǧ�ˣ������۸�����ͬ��
Ԫ/ǧ�ˣ������۸�����ͬ��
![]() �ҹ涨����������������
�ҹ涨����������������![]() ǧ�ˣ������ۼ۵�
ǧ�ˣ������ۼ۵�![]() �Żݣ���������������
�Żݣ���������������![]() ǧ�ˣ������ۼ۵�
ǧ�ˣ������ۼ۵�![]() �Żݣ�����
�Żݣ�����![]() ǧ�˵İ����ۼ۵�
ǧ�˵İ����ۼ۵�![]() �Żݡ�
�Żݡ�
![]() �ҵĹ涨���±���
�ҵĹ涨���±���
������Χ��ǧ�ˣ� |
|
|
|
|
�۸�Ԫ�� | ���ۼ۵� | ���ۼ۵� | ���ۼ۵� | ���ۼ۵� |
��![]() �����������
�����������![]() ǧ��ƻ����������
ǧ��ƻ����������![]() ��
��![]() ���������ֱ���Ҫ����Ԫ��
���������ֱ���Ҫ����Ԫ��
��![]() �����������
�����������![]() ǧ��ƻ��
ǧ��ƻ��![]() ������ֱ��ú�
������ֱ��ú�![]() �Ĵ���ʽ��ʾ����
�Ĵ���ʽ��ʾ����![]() ��
��![]() ������������Ҫ�ķ��ã�
������������Ҫ�ķ��ã�
��![]() ��������Ҫ����
��������Ҫ����![]() ǧ��ƻ�������ܰ�����ѡ�����ļ��������Ż�����˵�����ɣ�
ǧ��ƻ�������ܰ�����ѡ�����ļ��������Ż�����˵�����ɣ�