题目内容
【题目】如图,小明同学在将一张矩形纸片ABCD的四个角向内折起时,发现恰好能拼成一个无缝隙无重叠的四边形EFGH.于是他测量出EH=12cm,EF=16cm,根据这两个数据他很快求出了边AD的长,则边AD的长是( ) 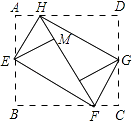
A.12cm
B.16cm
C.20cm
D.28cm
【答案】C
【解析】解:∵∠HEM=∠AEH,∠BEF=∠FEM, ∴∠HEF=∠HEM+∠FEM= ![]() ×180°=90°,
×180°=90°,
同理可得:∠EHG=∠HGF=90°,
∴四边形EFGH为矩形.
∴EH=FG,EH∥FG,
∴∠EHF=∠HFG,
∵∠AHE=∠EHF,∠CFG=∠HFG,
∴∠AHE=∠CFG,
∵∠A=∠C,
∴△AHE≌△CFG,
∴AH=CF,
∴AH=CF=FP,
∵HD=HP,
∴AD=AH+HD=PF+HP=HF,
∵HF= ![]() =
= ![]() =20,
=20,
∴AD=20cm,
故选C.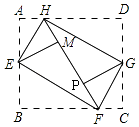
利用三个角是直角的四边形是矩形易证四边形EFGH为矩形,那么由折叠可得HF的长即为边AD的长.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目