题目内容
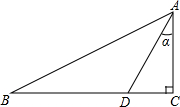
如图，在Rt△ABC中，∠C=90°，D是BC边上一点，AC=2，CD=1，设∠CAD=α．
（1）求sinα的值；
（2）若∠B=∠CAD，求BD的长．
（1）求sinα的值；
（2）若∠B=∠CAD，求BD的长．
在Rt△ACD中，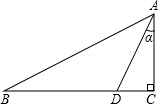
∵AC=2，DC=1，
∴AD=
=
=
．
（1）sinα=
=
=
；
答：sinα的值是
；
（2）∵∠B=∠CAD，
∴在Rt△ABC中，sinB=sinα=
，即
=
，
∴AB=
AC=2
，
∴BC=
=
=4，
∴BD=BC-CD=4-1=3．
答：BD的长度是3．
∵AC=2，DC=1，
∴AD=
| AC2+CD2 |
| 22+12 |
| 5 |
（1）sinα=
| CD |
| AD |
| 1 | ||
|
| ||
| 5 |
答：sinα的值是
| ||
| 5 |
（2）∵∠B=∠CAD，
∴在Rt△ABC中，sinB=sinα=
| ||
| 5 |
| AC |
| AB |
| ||
| 5 |
∴AB=
| 5 |
| 5 |
∴BC=
| AB2-AC2 |
| 20-4 |
∴BD=BC-CD=4-1=3．
答：BD的长度是3．
练习册系列答案
相关题目
方程x2-7x+12=0的两个根，且OA＞OB；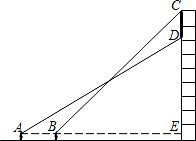
45°．若该楼高为26.65m，小杨的眼睛离地面1.65m，广告屏幕的上端与楼房的顶端平齐．求广告屏幕上端与下端之间的距离．（
