题目内容
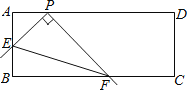
【题目】如图,已知点C在⊙O上,AC=![]() AB,动点P与点C位于直径AB的异侧,点P在半圆弧AB上运动(不与A.B两点重合),连结BP,过点C作直线PB的垂线CD交直线PB于D点,连结CP.
AB,动点P与点C位于直径AB的异侧,点P在半圆弧AB上运动(不与A.B两点重合),连结BP,过点C作直线PB的垂线CD交直线PB于D点,连结CP.
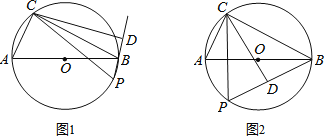
(1)如图1,在点P运动过程中,求∠CPD的度数;
(2)如图2,在点P运动过程中,当CP⊥AB时,AC=2时,求△BPC的周长
【答案】(1)60°;(2)![]()
【解析】
(1)由AC=![]() AB,动点P与点C位于直径AB的异侧,以求得∠ABC=30°,继而可得出∠ CPD的度数;(2)先证明△ CBP是等边三角形,再求出BC的长,最后求出△ CBP的周长
AB,动点P与点C位于直径AB的异侧,以求得∠ABC=30°,继而可得出∠ CPD的度数;(2)先证明△ CBP是等边三角形,再求出BC的长,最后求出△ CBP的周长
(1) ∵AB是直径,
∴∠ACB=90°,
∵AC=![]() AB,
AB,
∴∠ABC=30°,
∴∠A=90°∠ABC=60°,
∴∠CPD=∠A=60°;
(2)∵∠A=60°
∴∠BPC=∠A=60°
∵PC⊥AB,AB是直径
∴![]() =
=![]()
∴∠ABP=∠ABC=30°
∴∠CPB=60°
∴△CBP是等边三角形
∴BP=BC=CP
∵AC=2
∴BC=![]() AC=
AC=![]()
∴△BCP的周长=BP+BC+CP=![]()

练习册系列答案
相关题目