Question

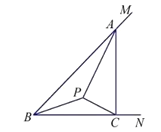
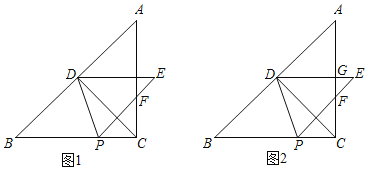
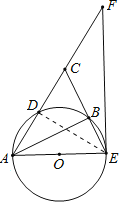
【题目】如图，在Rt△ABC中，∠ABC=90，D是AC的中点，⊙O经过A、B、D三点，CB的延长线交⊙O于点E．

(1)求证:AE=CE ．

(2)若EF与⊙O相切于点E，交AC的延长线于点F，且CD=CF=2cm，求⊙O的直径．

(3)若EF与⊙O相切于点E，点C在线段FD上，且CF:CD=2:1，求sin∠CAB ．

Answer 1

【答案】（1）见解析；（2）2cm；（3）

【解析】

（1）连接DE，根据可知：是直径，可得，结合点D是AC的中点，可得出ED是AC的中垂线，从而可证得结论；

（2）根据，可将AE解出，即求出⊙O的直径；

（3）根据等角代换得出，然后根据CF:CD=2:1，可得AC=CF，继而根据斜边中线等于斜边一半得出，在中，求出sin∠CAB即可．

证明：（1）连接，

，

，

∴是直径

∴，即，

又∵ 是的中点，

∴是的垂直平分线，

∴；

（2）在 和中，

，

故可得，

从而 ，即，

解得：AE=2；

即⊙O的直径为2．

（3），

，

， 是的中点，

，

，

在中，．

故可得．