题目内容
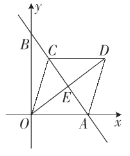
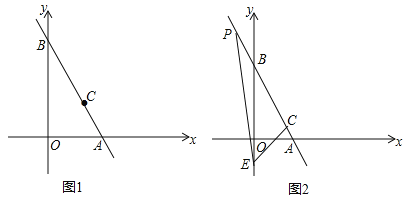
【题目】如图1,在平面直角坐标系中,直线AB经过点C(a,a),且交x轴于点A(m,0),交y轴于点B(0,n),且m,n满足![]() +(n﹣12)2=0.
+(n﹣12)2=0.
(1)求直线AB的解析式及C点坐标;
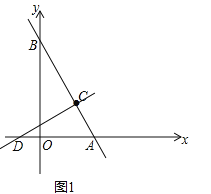
(2)过点C作CD⊥AB交x轴于点D,请在图1中画出图形,并求D点的坐标;
(3)如图2,点E(0,﹣2),点P为射线AB上一点,且∠CEP=45°,求点P的坐标.
【答案】(1)y=-2x+12,点C坐标(4,4);(2)画图形见解析,点D坐标(-4,0);(3)点P的坐标(![]() ,
,![]() )
)
【解析】
(1)由已知的等式可求得m、n的值,于是可得直线AB的函数解析式,把点C的坐标代入可求得a的值,由此即得答案;
(2)画出图象,由CD⊥AB知![]() 可设出直线CD的解析式,再把点C代入可得CD的解析式,进一步可求D点坐标;
可设出直线CD的解析式,再把点C代入可得CD的解析式,进一步可求D点坐标;
(3)如图2,取点F(-2,8),易证明CE⊥CF且CE=CF,于是得∠PEC=45°,进一步求出直线EF的解析式,再与直线AB联立求两直线的交点坐标,即为点P.
解:(1)∵![]() +(n﹣12)2=0,
+(n﹣12)2=0,
∴m=6,n=12,
∴A(6,0),B(0,12),
设直线AB解析式为y=kx+b,
则有![]() ,解得
,解得![]() ,
,
∴直线AB解析式为y=-2x+12,
∵直线AB过点C(a,a),
∴a=-2a+12,∴a=4,
∴点C坐标(4,4).
(2)过点C作CD⊥AB交x轴于点D,如图1所示,
设直线CD解析式为y=![]() x+b′,把点C(4,4)代入得到b′=2,
x+b′,把点C(4,4)代入得到b′=2,
∴直线CD解析式为y=![]() x+2,
x+2,
∴点D坐标(-4,0).
(3)如图2中,取点F(-2,8),作直线EF交直线AB于P,
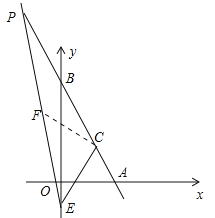
图2
∵直线EC解析式为y=![]() x-2,直线CF解析式为y=-
x-2,直线CF解析式为y=-![]() x+
x+![]() ,
,
∵![]() ×(-
×(-![]() )=-1,
)=-1,
∴直线CE⊥CF,
∵EC=2![]() ,CF=2
,CF=2![]() ,
,
∴EC=CF,
∴△FCE是等腰直角三角形,
∴∠FEC=45°,
∵直线FE解析式为y=-5x-2,
由![]() 解得
解得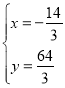 ,
,
∴点P的坐标为(![]() ).
).

【题目】从甲地到乙地有A,B,C三条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
公交车用时 公交车用时的频数 线路 |
|
|
|
| 合计 |
A | 59 | 151 | 166 | 124 | 500 |
B | 50 | 50 | 122 | 278 | 500 |
C | 45 | 265 | 167 | 23 | 500 |
早高峰期间,乘坐_________(填“A”,“B”或“C”)线路上的公交车,从甲地到乙地“用时不超过45分钟”的可能性最大.