题目内容
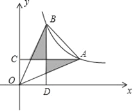
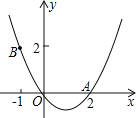
【题目】如图,抛物线y=ax2+bx(a>0)经过原点O和点A(2,0).
(1)写出抛物线的对称轴与x轴的交点坐标;
(2)点(x1,y1),(x2,y2)在抛物线上,若x1<x2<1,比较y1,y2的大小;
(3)点B(﹣1,2)在该抛物线上,点C与点B关于抛物线的对称轴对称,求直线AC的函数关系式.
【答案】(1)交点坐标(1,0)。
(2)y1>y2。
(3)y=2x﹣4。
【解析】
试题(1)根据图示可以直接写出抛物线的对称轴与x轴的交点坐标。
(2)根据抛物线的对称轴与x轴的交点坐标可以求得该抛物线的对称轴是x=1,然后根据函数图象的增减性进行解题。
(3)根据已知条件可以求得点C的坐标是(3,2),所以根据点A、C的坐标来求直线AC的函数关系式。
解:(1)根据图示,由抛物线的对称性可知,抛物线的对称轴与x轴的交点坐标(1,0)。
(2)抛物线的对称轴是直线x=1.
根据图示知,当x<1时,y随x的增大而减小,
∴当x1<x2<1时,y1>y2。
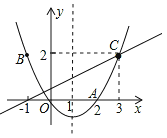
(3)∵对称轴是x=1,点B(﹣1,2)在该抛物线上,点C与点B关于抛物线的对称轴对称,
∴点C的坐标是(3,2)。
设直线AC的关系式为y=kx+b(k≠0),则
![]() ,解得
,解得![]() 。
。
∴直线AC的函数关系式是:y=2x﹣4。

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目