题目内容
【题目】如图,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() .
.![]() 是边
是边![]() 的中点,联结
的中点,联结![]() 、
、![]() ,且
,且![]() .设
.设![]() ,
,![]() .
.


(1)如果![]() ,求
,求![]() 的长;
的长;
(2)求![]() 关于
关于![]() 的函数解析式,并写出自变量
的函数解析式,并写出自变量![]() 的取值范围;
的取值范围;
(3)联结![]() .如果
.如果![]() 是以边
是以边![]() 为腰的等腰三角形,求
为腰的等腰三角形,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ,自变量
,自变量![]() 的取值范围是
的取值范围是![]() ,且
,且![]() ;(3)
;(3)![]()
【解析】
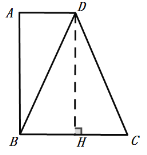
(1)首先过点D作DH⊥BC,垂足为点H,由AD∥BC,AB⊥BC,DH⊥BC,可求得DH的长,然后设CH=![]() ,则CD=2
,则CD=2![]() ,利用勾股定理即可求得答案;
,利用勾股定理即可求得答案;
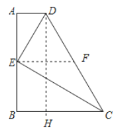
(2)首先取CD的中点F,连接EF,由梯形的中位线,可表示出EF的长,易得四边形ABHD是平行四边形,然后由勾股定理可求得答案;
(3)分别从CD=BD或CD=BC去分析求解即可求得答案.
(1)过点![]() 作
作![]() ,垂足为点
,垂足为点![]() .
.
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
在![]() 中,
中,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
设![]() ,则
,则![]() ,
,
利用勾股定理,得![]() .
.
即得![]() ,
,
解得![]() (负值舍去).
(负值舍去).
∴![]() ;
;
(2)取CD的中点F,连接EF,

∵![]() 为边
为边![]() 的中点,
的中点,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
由![]() ,
,![]() ,得
,得![]() .
.
∴![]() .
.
又∵![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,
即得![]() ,
,
在![]() 中,利用勾股定理,得
中,利用勾股定理,得![]() .
.
即得![]() .
.
解得![]() .
.
∴所求函数解析式为![]() .
.
自变量![]() 的取值范围是
的取值范围是![]() ,且
,且![]() .
.
(3)当![]() 是以边
是以边![]() 为腰的等腰三角形时,有两种可能情况:
为腰的等腰三角形时,有两种可能情况:
![]() 或
或![]() .
.
①如果![]() ,
,
作![]() 于H,
于H,
∴![]() ,
,
即得![]() ,
,
∵![]() ,
,
∴![]() .
.
解得![]() ,
,![]() .
.
经检验:![]() ,
,![]() ,是方程的解,
,是方程的解,
但![]() 不合题意,舍去.
不合题意,舍去.
∴![]() ;
;
②如果![]() ,则
,则![]() .
.
即得![]() (不合题意,舍去).
(不合题意,舍去).
综上,如果![]() 是以边
是以边![]() 为腰的等腰三角形,
为腰的等腰三角形,![]() 的值为
的值为![]() .
.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目