ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌжБЯпCBЁЮOAЃЌЁЯCЃНЁЯOABЃН100ЁуЃЌEЁЂFдкCBЩЯЃЌЧвТњзуЁЯFOBЃНЁЯAOBЃЌOEЦНЗжЁЯCOF
ЃЈ1ЃЉЧѓЁЯEOBЕФЖШЪ§ЃЛ
ЃЈ2ЃЉШєЦНаавЦЖЏABЃЌФЧУДЁЯOBCЃКЁЯOFCЕФжЕЪЧЗёЫцжЎЗЂЩњБфЛЏЃПШєБфЛЏЃЌевГіБфЛЏЙцТЩЛђЧѓГіБфЛЏЗЖЮЇЃЛШєВЛБфЃЌЧѓГіетИіБШжЕЃЎ
ЃЈ3ЃЉдкЦНаавЦЖЏABЕФЙ§ГЬжаЃЌЪЧЗёДцдкФГжжЧщПіЃЌЪЙЁЯOECЃНЁЯOBAЃПШєДцдкЃЌЧѓГіЦфЖШЪ§ЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
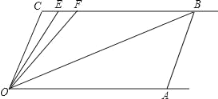
ЁОД№АИЁПЃЈ1ЃЉ40ЁуЃЛЃЈ2ЃЉЁЯOBCЃКЁЯOFCЃН1ЃК2ЃЌЪЧЖЈжЕЃЛЃЈ3ЃЉ60Ёу
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнСНжБЯпЦНааЃЌЭЌХдФкНЧЛЅВЙЧѓГіЁЯAOCЃЌШЛКѓЧѓГіЁЯEOBЃН![]() ЁЯAOCЃЌМЦЫуМДПЩЕУНтЃЛ
ЁЯAOCЃЌМЦЫуМДПЩЕУНтЃЛ
ЃЈ2ЃЉИљОнСНжБЯпЦНааЃЌФкДэНЧЯрЕШПЩЕУЁЯAOBЃНЁЯOBCЃЌдйИљОнШ§НЧаЮЕФвЛИіЭтНЧЕШгкгыЫќВЛЯрСкЕФСНИіФкНЧЕФКЭПЩЕУЁЯOFCЃН2ЁЯOBCЃЌДгЖјЕУНтЃЛ
ЃЈ3ЃЉИљОнШ§НЧаЮЕФФкНЧКЭЖЈРэЧѓГіЁЯCOEЃНЁЯAOBЃЌДгЖјЕУЕНOBЁЂOEЁЂOFЪЧЁЯAOCЕФЫФЕШЗжЯпЃЌдйРћгУШ§НЧаЮЕФФкНЧКЭЖЈРэСаЪНМЦЫуМДПЩЕУНтЃЎ
НтЃКЃЈ1ЃЉЁпCBЁЮOAЃЌ
ЁрЁЯAOCЃН180ЁуЉЁЯCЃН180ЁуЉ100ЁуЃН80ЁуЃЌ
ЁпOEЦНЗжЁЯCOFЃЌ
ЁрЁЯCOEЃНЁЯEOFЃЌ
ЁпЁЯFOBЃНЁЯAOBЃЌ
ЁрЁЯEOBЃНЁЯEOF+ЁЯFOBЃН![]() ЁЯAOCЃН
ЁЯAOCЃН![]() ЁС80ЁуЃН40ЁуЃЛ
ЁС80ЁуЃН40ЁуЃЛ
ЃЈ2ЃЉЁпCBЁЮOAЃЌ
ЁрЁЯAOBЃНЁЯOBCЃЌ
ЁпЁЯFOBЃНЁЯAOBЃЌ
ЁрЁЯFOBЃНЁЯOBCЃЌ
ЁрЁЯOFCЃНЁЯFOB+ЁЯOBCЃН2ЁЯOBCЃЌ
ЁрЁЯOBCЃКЁЯOFCЃН1ЃК2ЃЌЪЧЖЈжЕЃЛ
ЃЈ3ЃЉдкЁїCOEКЭЁїAOBжаЃЌ
ЁпЁЯOECЃНЁЯOBAЃЌЁЯCЃНЁЯOABЃЌ
ЁрЁЯCOEЃНЁЯAOBЃЌ
ЁрOBЁЂOEЁЂOFЪЧЁЯAOCЕФЫФЕШЗжЯпЃЌ
ЁрЁЯCOEЃН![]() ЁЯAOCЃН
ЁЯAOCЃН![]() ЁС80ЁуЃН20ЁуЃЌ
ЁС80ЁуЃН20ЁуЃЌ
ЁрЁЯOECЃН180ЁуЉЁЯCЉЁЯCOEЃН180ЁуЉ100ЁуЉ20ЁуЃН60ЁуЃЌ
ЙЪДцдкФГжжЧщПіЃЌЪЙЁЯOECЃНЁЯOBAЃЌДЫЪБЁЯOECЃНЁЯOBAЃН60ЁуЃЎ

 гХАйЗжПЮЪБЛЅЖЏЯЕСаД№АИ
гХАйЗжПЮЪБЛЅЖЏЯЕСаД№АИ