题目内容
【题目】在矩形ABCD中,AC、BD交于点O,点P、E分别是直线BD、BC上的动点,且PE=PC,过点E作EF∥AC交直线BD于点F.


(1)如图1,当∠COD=90°时,判断△BEF的形状,并说明理由;
(2)如图2,当点P在线段BO上时,求证:OP=BF;
(3)当∠COD=60°,CD=3时,请直接写出当△PEF成为直角三角形时的面积.
【答案】(1)△BEF是等腰直角三角形,理由见解析;(2)见解析;(3)当△PEF成为直角三角形时的面积是![]() .
.
【解析】
(1)根据对角线互相垂直的矩形是正方形判定矩形ABCD是正方形,再由平行线的性质和正方形的性质得∠FEB=45°,从而得:△BEF是等腰直角三角形;
(2)根据AAS证明△PEF≌△COP,可得结论;
(3)根据∠COD=60°,得△COD是等边三角形,则OC=CD=3,证明△PFE≌△COP(ASA),得PF=OC=3,根据直角三角形30度角的性质计算PE和EF的长,根据三角形的面积公式可得结论.
(1)△BEF是等腰直角三角形.
理由是:
如图1,∵∠COD=90°,
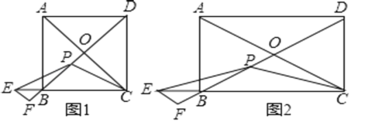
∴AC⊥BD,
∴矩形ABCD是正方形,
∴∠ACB=45°,
∵EF∥AC,
∴∠FEB=∠ACB=45°,∠F=∠BOC=90°,
∴△BEF是等腰直角三角形.
(2)如图2,∵四边形ABCD是矩形,
∴AC=BD,OB=![]() BD,OC=
BD,OC=![]() AC,
AC,
∴OB=OC,
∴∠OBC=∠OCB
∵PE=PC,
∴∠BEP=∠PCB,
∵∠OBC=∠BEP+∠EPB,∠OCB=∠PCB+∠OCP,
∴∠EPB=∠OCP
∵EF∥AC,
∴∠COP=∠BFE,
∴△PEF≌△CPO(AAS),
∴OC=PF=OB,
∴OB﹣PB=PF﹣PB,
即OP=BF
(3)∵四边形ABCD是矩形,
∴AC=BD,OD=![]() BD,OC=
BD,OC=![]() AC,
AC,
∴OD=OC,
∵∠COD=60°,
∴△COD是等边三角形,
∴OC=CD=3,
如图3,当∠PEF=90°时,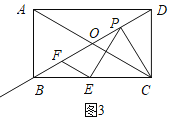
∵EF∥AC,
∴∠POC=∠OFE=60°,
∴∠BFE=120°,
∴OB=OC,
∴∠OBC=∠OCB=∠FEB=30°,
∵∠FEP=90°,
∴∠PEC=60°,
∵PE=PC,
∴△PEC是等边三角形,
∴∠PCB=60°,
∴∠PCO=60°-30°=30°=∠FPE,
∴△PFE≌△COP(ASA),
∴PF=OC=3,
Rt△PFE中,EF=![]() ,PE=
,PE=![]() ,
,
∴S△PEF=![]() EFPE=
EFPE=![]() ×
×![]() ×
×![]() =
=![]() ;
;
∴当△PEF成为直角三角形时的面积是![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案