Question

【题目】如图，在⊙O中，点C是直径AB延长线上一点，过点C作⊙O的切线，切点为D，连结BD．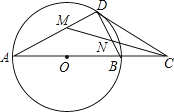
（1）求证：∠A=∠BDC；
（2）若CM平分∠ACD，且分别交AD、BD于点M、N，当DM=1时，求MN的长．

Answer 1

【答案】
（1）

证明：如图，连接OD，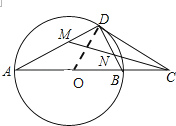

∵AB为⊙O的直径，

∴∠ADB=90°，即∠A+∠ABD=90°，

又∵CD与⊙O相切于点D，

∴∠CDB+∠ODB=90°，

∵OD=OB，

∴∠ABD=∠ODB，

∴∠A=∠BDC．

（2）

解：∵CM平分∠ACD，

∴∠DCM=∠ACM，

又∵∠A=∠BDC，

∴∠A+∠ACM=∠BDC+∠DCM，即∠DMN=∠DNM，

∵∠ADB=90°，DM=1，

∴DN=DM=1，

∴MN= =

【解析】（1）由圆周角推论可得∠A+∠ABD=90°，由切线性质可得∠CDB+∠ODB=90°，而∠ABD=∠ODB，可得答案；
　　　　（2）由角平分线及三角形外角性质可得∠A+∠ACM=∠BDC+∠DCM，即∠DMN=∠DNM，根据勾股定理可求得MN的长．本题主要考查切线的性质、圆周角定理、角平分线的性质及勾股定理，熟练掌握切线的性质：圆的切线垂直于过切点的半径是解本题的关键．
【考点精析】根据题目的已知条件，利用切线的性质定理的相关知识可以得到问题的答案，需要掌握切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径．