题目内容
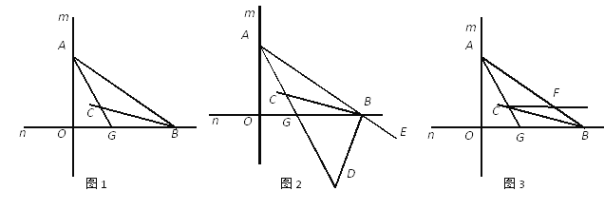
【题目】对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如图1可以得到![]() ,请解答下列问题:
,请解答下列问题:

(1)图2所表示的数学等式为_____________________;
(2)利用(1)得到的结论,解决问题: 若![]() ,求
,求![]() 的值;
的值;
(3)如图3,将两个边长分别为a和b的正方形拼在一起,![]() 三点在同一直线上,连接
三点在同一直线上,连接![]() ,若两正方形的边长满足
,若两正方形的边长满足![]()
![]() 求阴影部分面积.
求阴影部分面积.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据面积的不同求解方法,可得到不同的表示方法.一种可以是3个正方形的面积和6个矩形的面积,另一种是大正方形的面积,可得等式(a+b+c)2=a2+b2+c2+2ab+2bc+2ac;
(2)利用(1)中的乘法公式,进行变形得出答案即可;
(3)利用S阴影=正方形ABCD的面积+正方形ECGF的面积-三角形EGF的面积-三角形AED的面积求解.
(1)由图可得,(a+b+c)2=a2+b2+c2+2ab+2bc+2ac;
故答案为:(a+b+c)2=a2+b2+c2+2ab+2bc+2ac;
(2)由(1)可得:ab+bc+ac=![]() [(a+b+c)2(a2+b2+c2)]=
[(a+b+c)2(a2+b2+c2)]= ![]() [12260]=42;
[12260]=42;
(3)S阴影=a2+b2![]() (ab)a
(ab)a![]() b2
b2
=a2+b2![]() a2+
a2+![]() ab
ab![]() b2
b2
=![]() (a2+b2+ab)
(a2+b2+ab)
=![]() [(a+b)2ab]
[(a+b)2ab]
=![]() [15235]
[15235]
=95.

练习册系列答案
相关题目