题目内容
如图,抛物线的顶点为A(2,1),且经过原点O,与x轴的另一个交点为B.
(1)求抛物线的解析式;
(2)在抛物线上求点M,使△MOB的面积是△AOB面积的3倍;
(3)在抛物线的对称轴上一点C,在抛物线上是否存在点P,使以O、B、P、C为顶点的四边形为平行四边形?若存在,求出P点的坐标;若不存在,说明理由.
分析:(1)设出抛物线的顶点式,代入原点坐标即可求出答案;
(2)由△AOB和所求△MOB同底不等高,得出△MOB的高是△AOB高的3倍,可知抛物线上点M的纵坐标,因此建立方程解答即可;
(3)由平行四边形的判定,对边平行且相等,进一步利用对称性即可解答.
(2)由△AOB和所求△MOB同底不等高,得出△MOB的高是△AOB高的3倍,可知抛物线上点M的纵坐标,因此建立方程解答即可;
(3)由平行四边形的判定,对边平行且相等,进一步利用对称性即可解答.
解答:解:(1)由题意,可设抛物线的解析式为y=a(x-2)2+1,
∵抛物线过原点,
∴a(0-2)2+1=0,
a=-
;
∴抛物线的解析式为y=-
(x-2)2+1=-
x2+x;
(2)△AOB和所求△MOB同底不等高,且S△MOB=3S△AOB,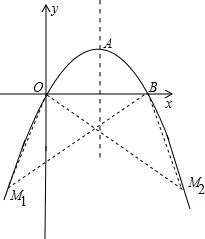
∴△MOB的高是△AOB高的3倍,即M点的纵坐标是-3,
∴-3=-
x2+x,
即x2-4x-12=0,
解得x1=6,x2=-2;
∴满足条件的点有两个:M1=(6,-3),M2=(-2,-3);
(3)存在;
由OB=CP=4,P的横坐标为6或-2,代入抛物线解析式得y=-
x2+x=-3,
P(6,-3)或(-2,-3),
当点C与点A重合时,点A关于x轴的对称点P(2,-1)也为所求,
因此存在,点P的坐标为P1(6,-3),P2(-2,-3),P3(2,-1).
∵抛物线过原点,
∴a(0-2)2+1=0,
a=-
| 1 |
| 4 |
∴抛物线的解析式为y=-
| 1 |
| 4 |
| 1 |
| 4 |
(2)△AOB和所求△MOB同底不等高,且S△MOB=3S△AOB,

∴△MOB的高是△AOB高的3倍,即M点的纵坐标是-3,
∴-3=-
| 1 |
| 4 |
即x2-4x-12=0,
解得x1=6,x2=-2;
∴满足条件的点有两个:M1=(6,-3),M2=(-2,-3);
(3)存在;

由OB=CP=4,P的横坐标为6或-2,代入抛物线解析式得y=-
| 1 |
| 4 |
P(6,-3)或(-2,-3),
当点C与点A重合时,点A关于x轴的对称点P(2,-1)也为所求,
因此存在,点P的坐标为P1(6,-3),P2(-2,-3),P3(2,-1).
点评:此题考查待定系数法求函数解析式,二次函数的对称性,三角形的面积以及平行四边形判定的运用,是一道综合性很强的题目.

练习册系列答案
相关题目
 点.
点. 21、如图,抛物线的顶点为A(1,-4),且过点B(3,0).
21、如图,抛物线的顶点为A(1,-4),且过点B(3,0). (2013•河南)如图,抛物线的顶点为P(-2,2),与y轴交于点A(0,3).若平移该抛物线使其顶点P沿直线移动到点P′(2,-2),点A的对应点为A′,则抛物线上PA段扫过的区域(阴影部分)的面积为
(2013•河南)如图,抛物线的顶点为P(-2,2),与y轴交于点A(0,3).若平移该抛物线使其顶点P沿直线移动到点P′(2,-2),点A的对应点为A′,则抛物线上PA段扫过的区域(阴影部分)的面积为 (2013•峨眉山市二模)已知,如图,抛物线的顶点为C(1,-2),直线y=kx+m与抛物线交于A、B两点,其中OA=3,B点在y轴上.点P为线段AB上的一个动点(点P与点A、B不重合),过点P且垂直于x轴的直线与这条抛物线交于点E.
(2013•峨眉山市二模)已知,如图,抛物线的顶点为C(1,-2),直线y=kx+m与抛物线交于A、B两点,其中OA=3,B点在y轴上.点P为线段AB上的一个动点(点P与点A、B不重合),过点P且垂直于x轴的直线与这条抛物线交于点E. (2013•鄂尔多斯)如图,抛物线的顶点为C(-1,-1),且经过点A、点B和坐标原点O,点B的横坐标为-3.
(2013•鄂尔多斯)如图,抛物线的顶点为C(-1,-1),且经过点A、点B和坐标原点O,点B的横坐标为-3.