题目内容
【题目】在△ABC和△A1B1C1中,下列命题中真命题的个数为( )
(1)若∠A=∠A1,∠C=∠C1,则△ABC∽△A1B1C1;
(2)若AC∶A1C1=CB∶C1B1,∠C=∠C1,则△ABC∽△A1B1C1;
(3)若AB=kA1B1,AC=kA1C1(k≠0),∠A=∠A1,则△ABC∽△A1B1C1;
(4)若S△ABC=![]() ,则△ABC∽△A1B1C1.
,则△ABC∽△A1B1C1.
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】
根据相似三角形的性质①有两角相等的两个三角形相似,②有两边的比相等,并且它们的夹角也相等的两个三角形相似,③有三组对应边的比相等的两三角形相似,逐个判断即可.
解:如图:
(1)![]() ∠A=∠
∠A=∠![]() ,∠C=∠
,∠C=∠![]() ,
,
![]() △ABC~△
△ABC~△![]() ,
,![]() (1)正确;
(1)正确;
(2)AC∶A1C1=CB∶C1B1,∠C=∠C1, ![]() △ABC~△
△ABC~△![]() ,(2)正确;
,(2)正确;
(3) ![]() AB=kA1B1,AC=kA1C1(k≠0),
AB=kA1B1,AC=kA1C1(k≠0),![]()
![]() =k
=k
又![]() ∠A=∠A1
∠A=∠A1![]() △ABC~△
△ABC~△![]() ,(3)正确;
,(3)正确;
(4)当AB=2,AB边上的高为1,![]() =1,
=1,![]() 边上的高为2时, S△ABC=
边上的高为2时, S△ABC=![]() 此时△ABC和△
此时△ABC和△![]() 不相似,故(4)错误;
不相似,故(4)错误;
所以正确的有(1)(2)(3),故C选项是正确的.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
【题目】某校积极开展“我爱我的祖国”教育知识竞赛,八年级甲、乙两班分别选5名同学参加比赛,其预赛成绩如图所示:
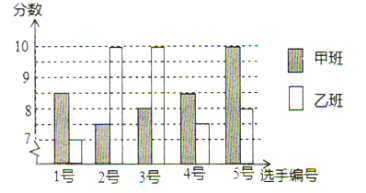
(1)根据上图填写下表:
平均数 | 中位数 | 众数 | 方差 | |
甲班 | 8.5 | |||
乙班 | 8.5 | 10 | 1.6 |
(2)根据上表数据,分别从平均数、中位数、众数、方差的角度对甲乙两班进行分析.